王家瑋,吳嘎日迪

(內(nèi)蒙古師范大學 數(shù)學科學學院,內(nèi)蒙古呼和浩特 010022;內(nèi)蒙古師范大學 應用數(shù)學中心,內(nèi)蒙古呼和浩特 010022)

§1 引言

本文用M(u)和N(v)表示互余的N函數(shù),關于N函數(shù)的定義及其性質(zhì)見文獻[1]中P1,由N函數(shù)M(u)生成的Orlicz空間[-π,π]是指具有有限的Orlicz范數(shù)

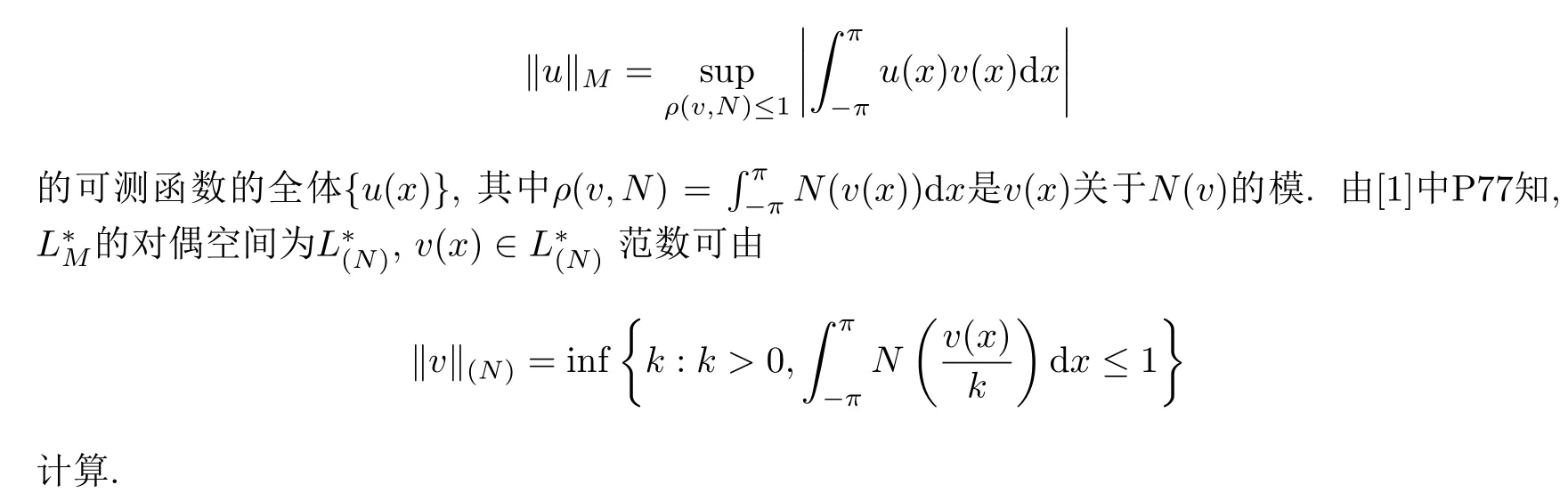
文中C表示常數(shù),且在不同處可取不同的值.

設Wr[-π,π]表示[-π,π]上r次非周期可微函數(shù)類,f(r-1)絕對連續(xù),且‖‖f(r)‖‖M ≤1.下面用Ls表示任一線性賦范空間,‖·‖表示該空間上的范數(shù).WrL*M[-π,π]在Ls下的n維Kolmogorov寬度,線性寬度,Gelfand寬度分別定義為[2,P298]

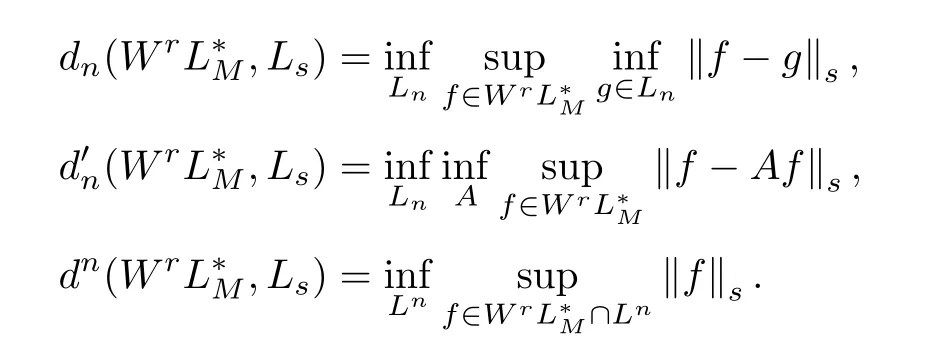
其中Ln ?Ls為Ls的任一n維子空間,Ln是Ls的n余維子空間,A是Wr →Ln的任一線性有界算子.

Lp空間中非周期類WrLp內(nèi)的函數(shù)可以分解為一個周期卷積函數(shù)加一個代數(shù)多項式的形式,若可解決相應的周期卷積函數(shù)類的寬度問題,那么非周期類的寬度問題也可得到解決,文獻[2]研究了周期可微函數(shù)類

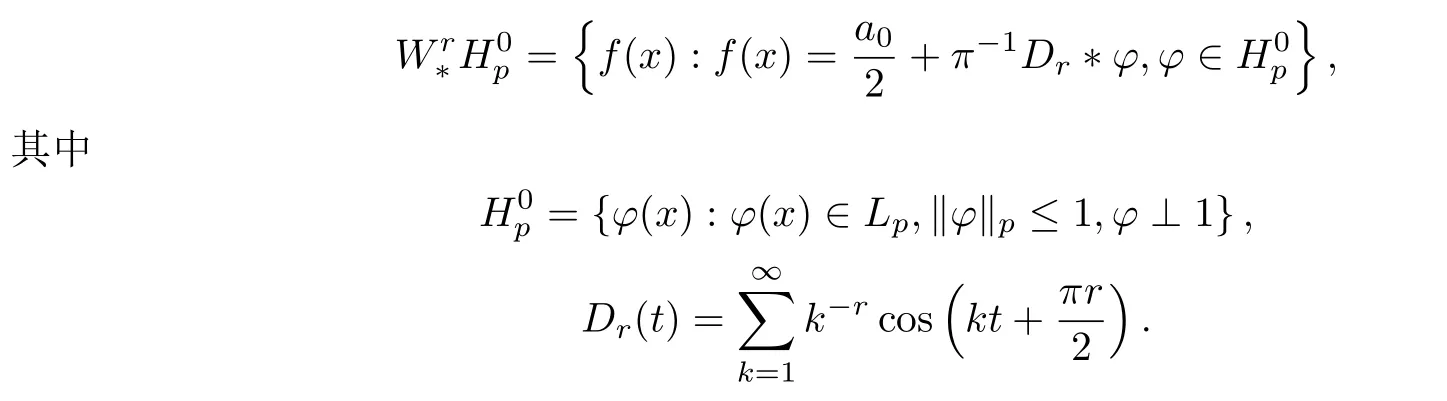
并得到以下兩個結果.

定理A

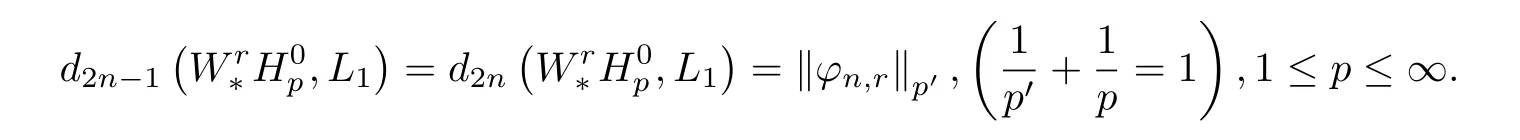
定理B

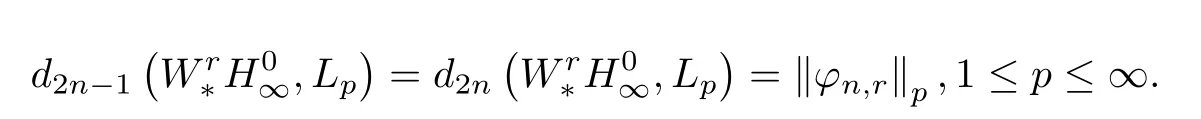
定理中φn,r均表示sign(sinnx)的r階周期積分,且滿足在周期上的平均值為零.

文獻[3]將上述結果推廣到非周期函數(shù)類上.本文將進一步研究Orlicz空間中定義域為[-π,π] 的非周期函數(shù)類Wr在L1內(nèi)Kolmogorov寬度的漸近精確估計及其漸近最優(yōu)子空間,并進一步討論Kolmogorov 寬度,線性寬度,Gelfand寬度的對偶形式.

下面引入Orlicz內(nèi)的周期函數(shù)類

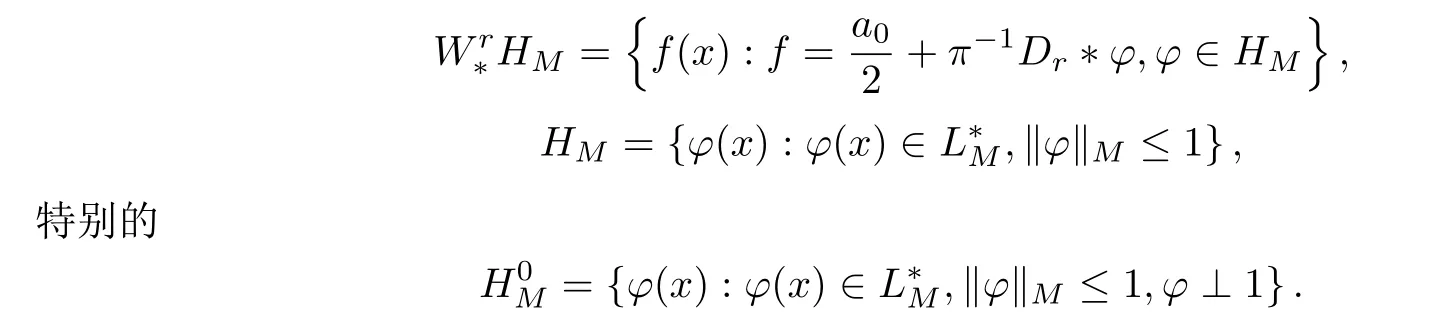
定義1.1X是一個Banach空間,其范數(shù)為‖·‖X,M?X是其中心對稱集,FN ?X為X的子空間,dim(FN)≤N.稱{FN}是M在X內(nèi)關于Kolmogorov寬度的漸近最優(yōu)子空間,如果

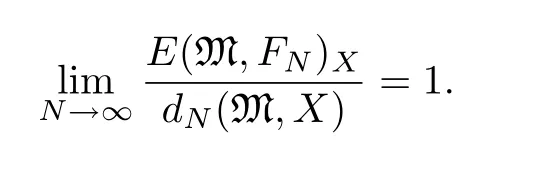
其中πr(x)是一個r次代數(shù)多項式.由此把非周期函數(shù)類WrL*M[-π,π]內(nèi)的函數(shù)進行了分解.

§2 主要結果

定理2.1dn(Wr,L1)≈2r‖φn,r‖(N)(n →∞).

證首先證明對于周期函數(shù)類有

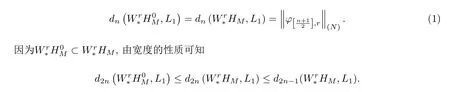
由文獻[4]中定理1結合文獻[5]的計算方法可得

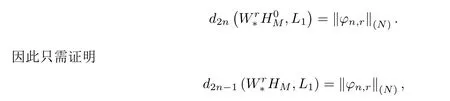
為此,取2n-1維三角多項式子空間,由文獻[2]中P64最佳逼近的對偶定理有

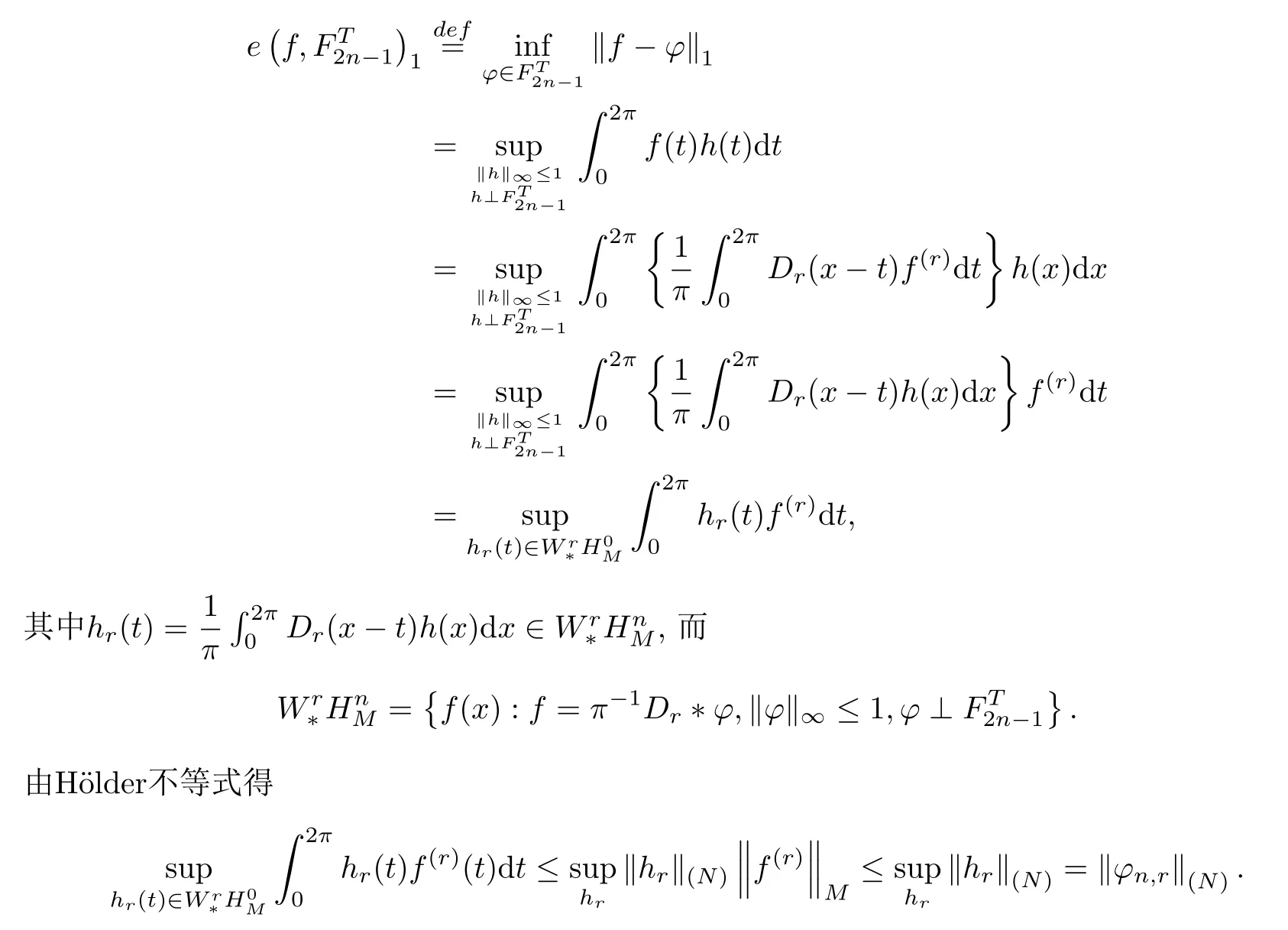
事實上,由文獻[6]可知上式中最后一個等號成立.由此可得

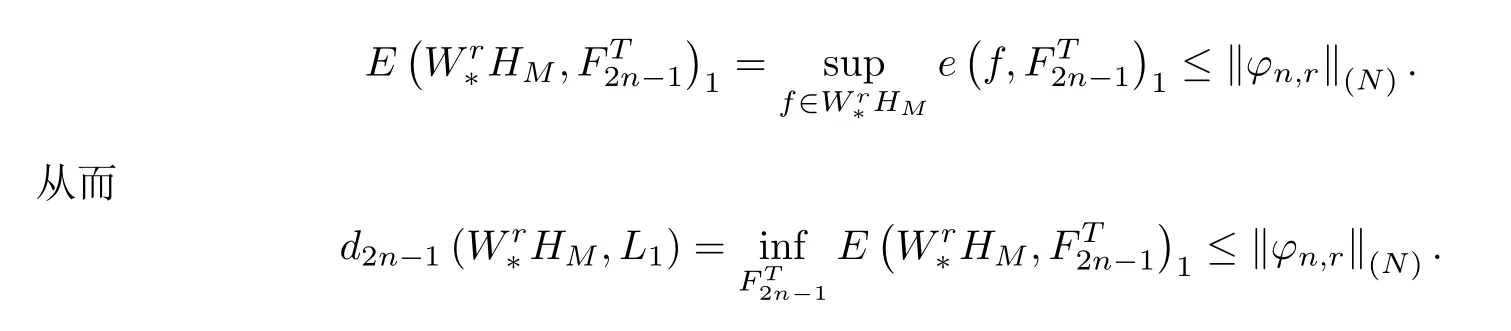
式(1)得證.

接下來考慮非周期函數(shù)類Wr.令Pr表示r次代數(shù)多項式子空間,且

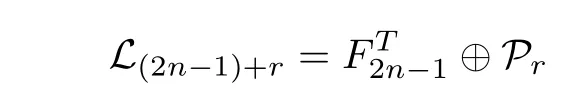
是L1[-π,π]內(nèi)(2n-1)+r維子空間,任取f ∈WrL*M[-π,π],由非周期函數(shù)類內(nèi)的函數(shù)分解式f=φ+πr,φ ∈HM與式(1)可得

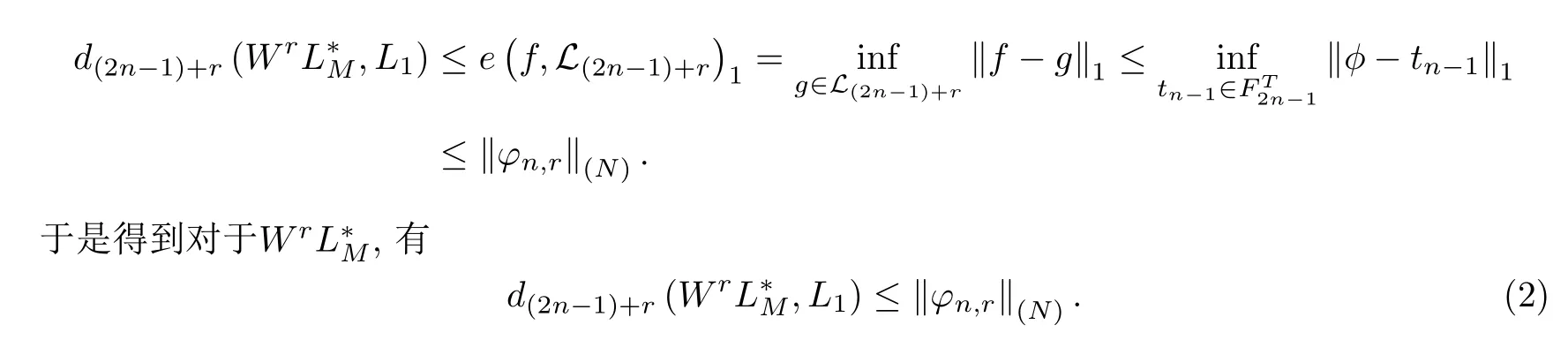
任取一自然數(shù)N ＞r使N -r為奇數(shù),由式(2)可知

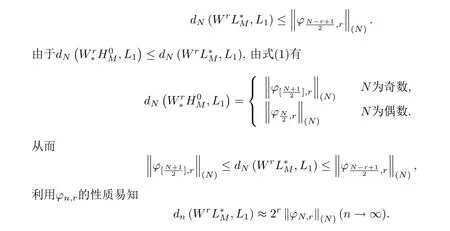
定理2.1得證.

定理2.1證明了L(2n-1)+r可以作為非周期函數(shù)類Wr的一個漸近最優(yōu)子空間,下面的定理將說明的漸近最優(yōu)子空間之間有著密切的關系.

定義2.1取

則有如下定理.

定理2.2L(2n+1)+r是Wr在L1內(nèi)的(2n+1)+r維漸近最優(yōu)子空間,即

另一方面,若hr(t)滿足補充條件

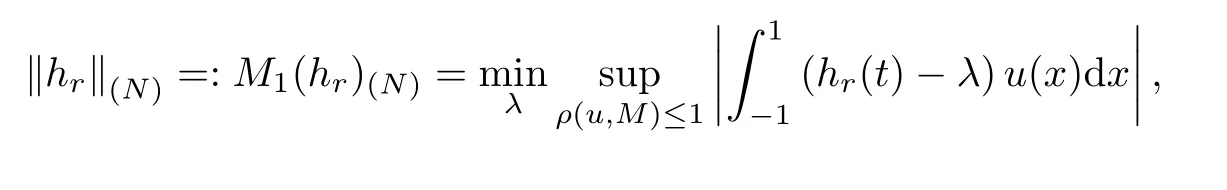
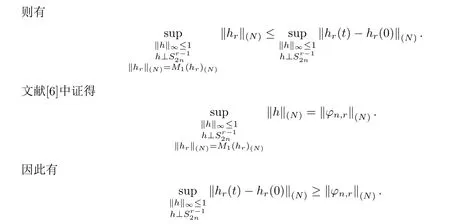
式(3)得證.

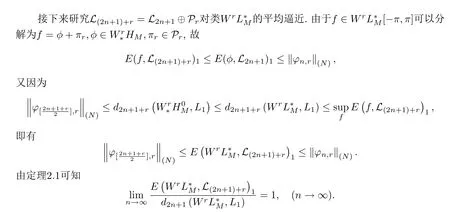
定理2.2證畢.

接下來考慮分別研究三種寬度的對偶形式.

定理2.3

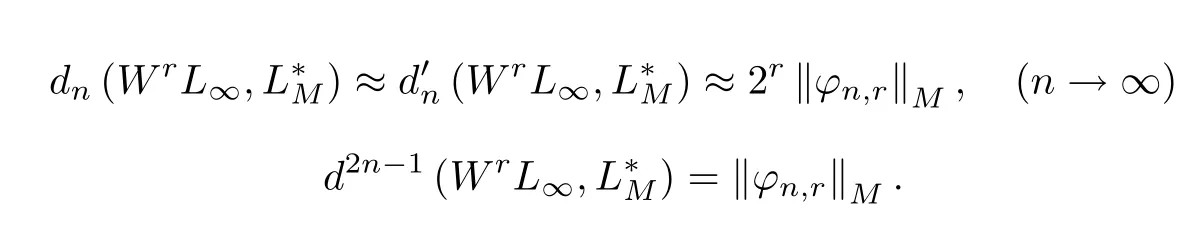
證由文獻[7]中結論結合文獻[5]中的方法可證得

其中Li(x)表示基本樣條,即Li(tk,r-1)=δi,k,(i,k=1,2,...,2n).

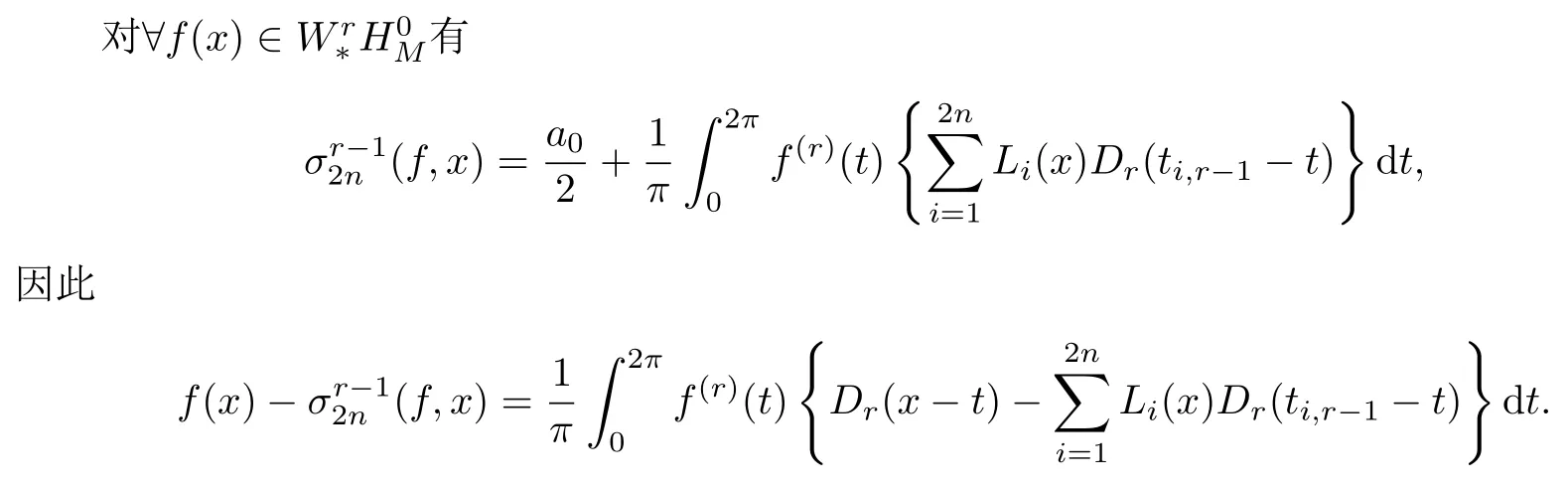
利用文獻[7]能夠證明可以找到一個函數(shù)Fn,r(x)使

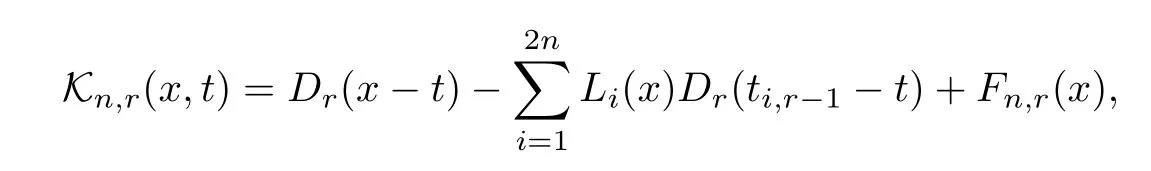
定義2.2Qn表示以2π為周期的函數(shù)類,且滿足對?f(x)∈Qn,存在點x0＜x1＜...＜xN=x0+2π,1≤N ≤2n.滿足對每一個區(qū)間[xi-1,xi]上f(x)=εi,εi=±1.

令f(x)∈Qn,且在區(qū)間[0,2π]上的平均值為0,令fr(x)為函數(shù)f(x)的r階周期積分,由文獻[4]的推論3可得

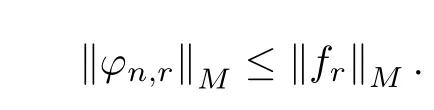
對中任意不包含常數(shù)的子空間L2n,由文獻[4],存在一個函數(shù)F(x)∈L2n滿足F(r)(x)∈Qn.于是

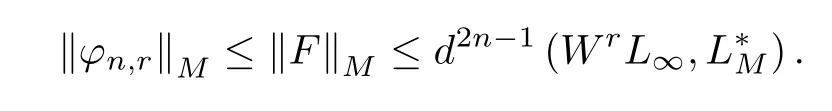
因此

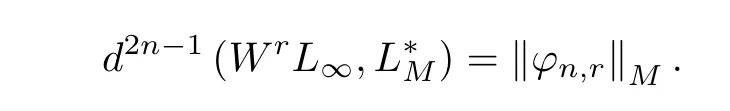
定理2.3證畢.