周海林

(南京理工大學(xué) 泰州科技學(xué)院,江蘇泰州 225300)

§1 引言

約束矩陣方程的最小二乘問題是指矩陣方程的最小二乘解需要滿足某一約束條件.不同的約束條件或不同的矩陣方程,就得到不同的約束矩陣方程的最小二乘問題.

約束矩陣方程的求解具有重要的理論意義和很高的應(yīng)用價(jià)值.來源于系統(tǒng)與控制理論中提出的矩陣方程AXB+CXD=F,在特征結(jié)構(gòu)配置[1],觀測器設(shè)計(jì)[2]和帶有輸入約束的系統(tǒng)控制[3]等方面起著重要的作用,也受到矩陣論和數(shù)值分析學(xué)者的關(guān)注,取得了一些成果[4-11].這些文獻(xiàn)主要應(yīng)用廣義逆,奇異值分解和廣義奇異值分解,得到了矩陣方程的解的充要條件及解析表達(dá)式.

迭代法是求解約束矩陣方程的另外一種方法,盡管它不能給出通解表達(dá)式,但在不考慮舍入誤差的情況下,能通過有限步迭代得到滿足給定約束條件的解.應(yīng)用共軛梯度法,文[12-14]構(gòu)造迭代算法分別求解了矩陣方程AXB+CXD=F的一般解,對稱解和在任意線性子空間約束下的解.文[15-17]研究了Hermitian解和極小范數(shù)最小二乘Hermitian解.更多求解矩陣方程AXB+CXD=F的迭代算法可參考文獻(xiàn)[18-28].

記Rm×n表示m×n實(shí)矩陣集合,AT表示A的轉(zhuǎn)置矩陣.對任意的矩陣A,B∈Rm×n,定義矩陣內(nèi)積〈A,B〉=tr(BTA),則由它誘導(dǎo)的范數(shù)為Frobenius范數(shù),即

本文主要考慮下面兩個(gè)問題.

問題I給定矩陣A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任意線性子空間R ?Rs×t,求X*∈R,使得

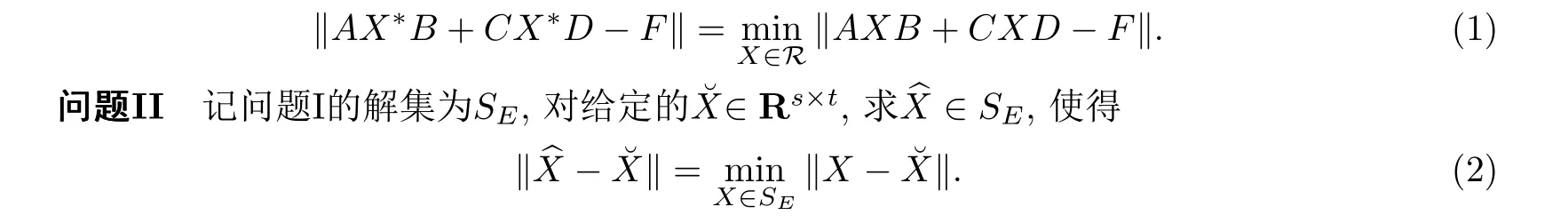
相應(yīng)地,問題I和問題II的解稱為矩陣方程AXB+CXD=F滿足線性子空間R約束條件下的最小二乘解和最佳逼近解.本文應(yīng)用共軛梯度法,結(jié)合線性投影算子,將負(fù)梯度到所求線性子空間上的投影矩陣作為迭代過程中下一步的更新矩陣,給出迭代算法,求解了矩陣方程AXB+CXD=F在任意線性子空間上的最小二乘解及其最佳逼近.

本文以下內(nèi)容安排如下:§2構(gòu)造迭代算法求解了問題I ;§3應(yīng)用問題I的算法進(jìn)一步求解了問題II;§4給出兩個(gè)數(shù)值例子證實(shí)了算法的有效性;§5對全文進(jìn)行了小結(jié).

§2 迭代求解問題I

定義2.1對矩陣M,N ∈Rm×n,若〈M,N〉=0,則稱矩陣M,N相互正交.

對任意的線性子空間R ?Rs×t,其正交補(bǔ)空間R⊥是存在唯一的,且有Rs×t=R ⊕R⊥.在Rs×t上定義線性投影算子FR:Rs×t -→R.

顯然,對任意的X∈Rs×t和任意的S∈R,有〈X,S〉=〈FR(X)+FR⊥(X),S〉=〈FR(X),S〉成立.

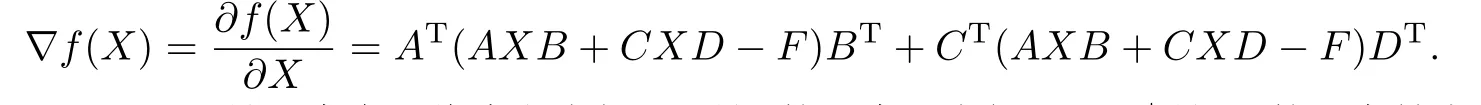
引理2.1設(shè)S是一個(gè)有限維內(nèi)積空間,M是S的一個(gè)子空間,且M⊥是M的正交補(bǔ)空間.則對于任意給定的向量s ∈S,必存在著唯一的向量m0∈M,使得

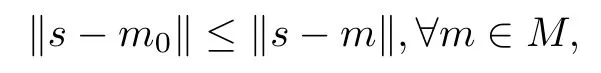
其中‖·‖是內(nèi)積空間S所定義的范數(shù),并且m0∈M是唯一的極小化向量的充要條件是(sm0)⊥M,即(s-m0)∈M⊥.

引理2.2設(shè)線性子空間R ?Rs×t,FR是從Rs×t到R的線性投影算子,記R*=F -(AX*B+CX*D),則X*是矩陣方程AXB+CXD=F在線性子空間R上的最小二乘解的充要條件是FR(?f(X*))=0.

證定義集合

顯然,L為線性子空間.假設(shè)矩陣X*∈R,記F*=AX*B+CX*D,則F* ∈L.由引理2.1知,X*是矩陣方程AXB+CXD=F的最小二乘解,當(dāng)且僅當(dāng)

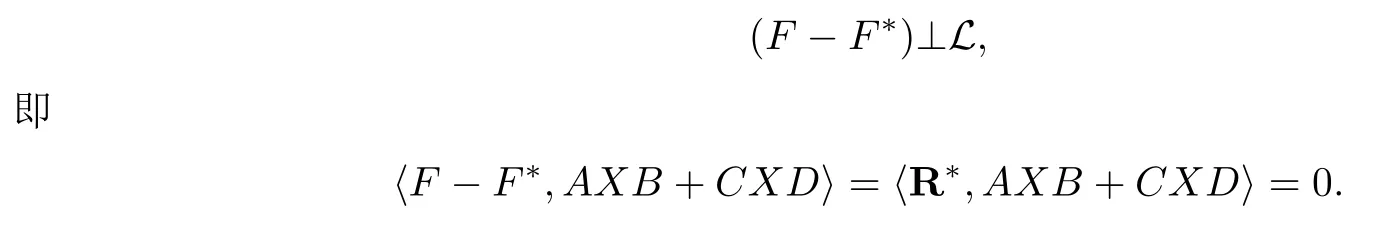
另外對任意的X ∈R有

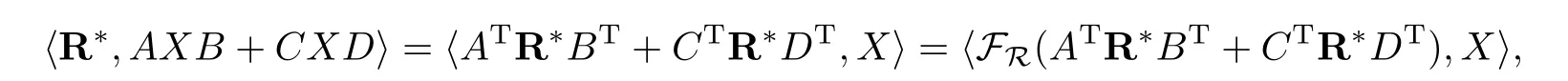
從而FR(ATR*BT+CTR*DT)=0,即有FR(?f(X*))=0,故引理得證.

應(yīng)用共軛梯度法,結(jié)合線性投影算子,本文構(gòu)造如下迭代算法.

算法I

輸入矩陣A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任取初始矩陣X0∈R.

(1) 計(jì)算

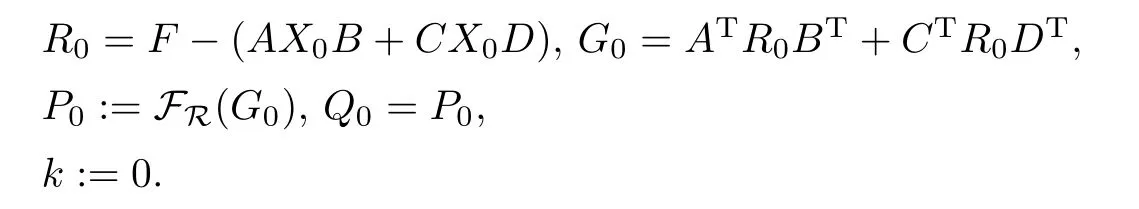
(2) 如果Pk=0,停止;否則進(jìn)行下一步.

(3) 計(jì)算

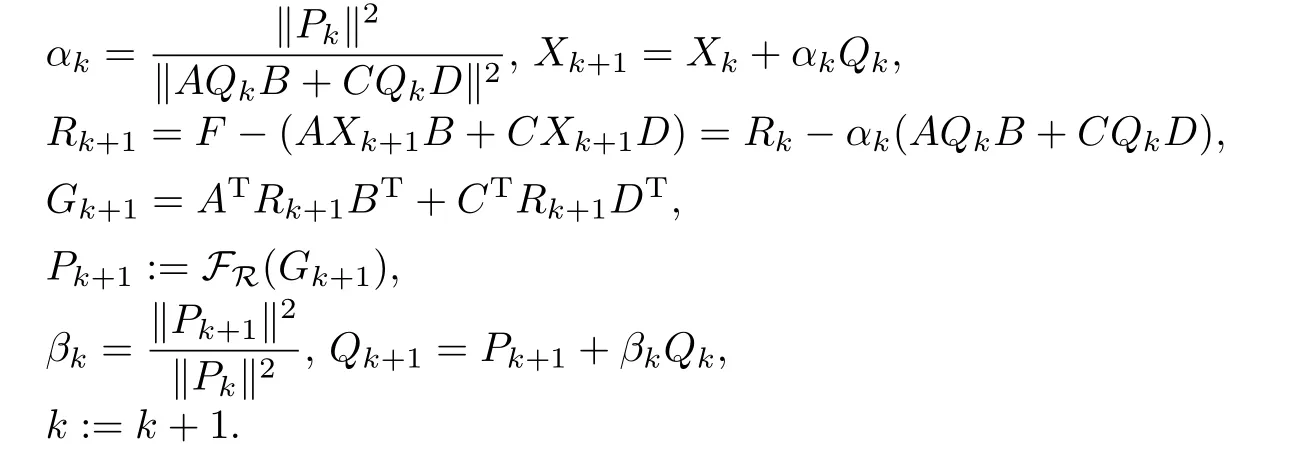
(4) 轉(zhuǎn)回到(2).

顯然,Pi=FR(ATRiBT+CTRiDT)=FR(-?f(X)|X=Xi)∈R,Qi ∈R,Xi ∈R,i=0,1,2,3,···.

此外在步驟(3)中

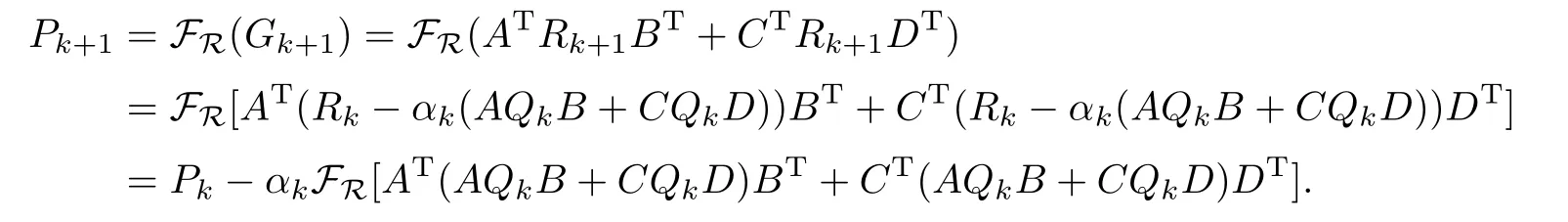
引理2.3若算法I在第k步迭代尚未停止,則迭代過程中產(chǎn)生的Pi,Pj,Qi,Qj,(i,j=0,1,21),有

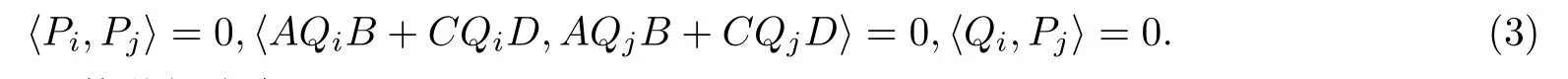
證用數(shù)學(xué)歸納法證明.

由于對任意矩陣M,N∈Rm×n,有〈M,N〉=〈N,M〉,故只需證明0≤i ＜j ≤k時(shí)結(jié)論成立即可.

首先注意到

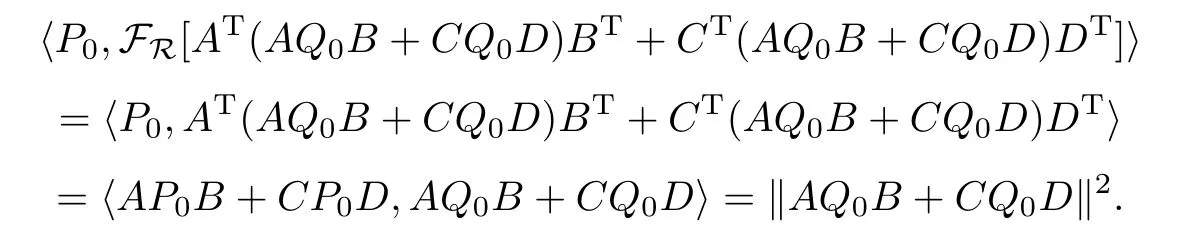
對t=1,由算法I有

設(shè)(3)式對t=s(1≤s ≤k-1)成立,即

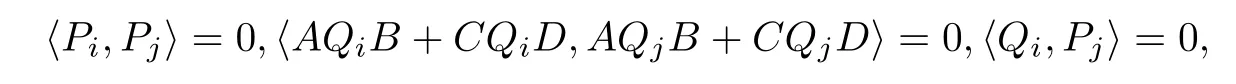
i,j=0,1,21,則當(dāng)t=s+1時(shí),由算法I,與(4)式相類似的證明有

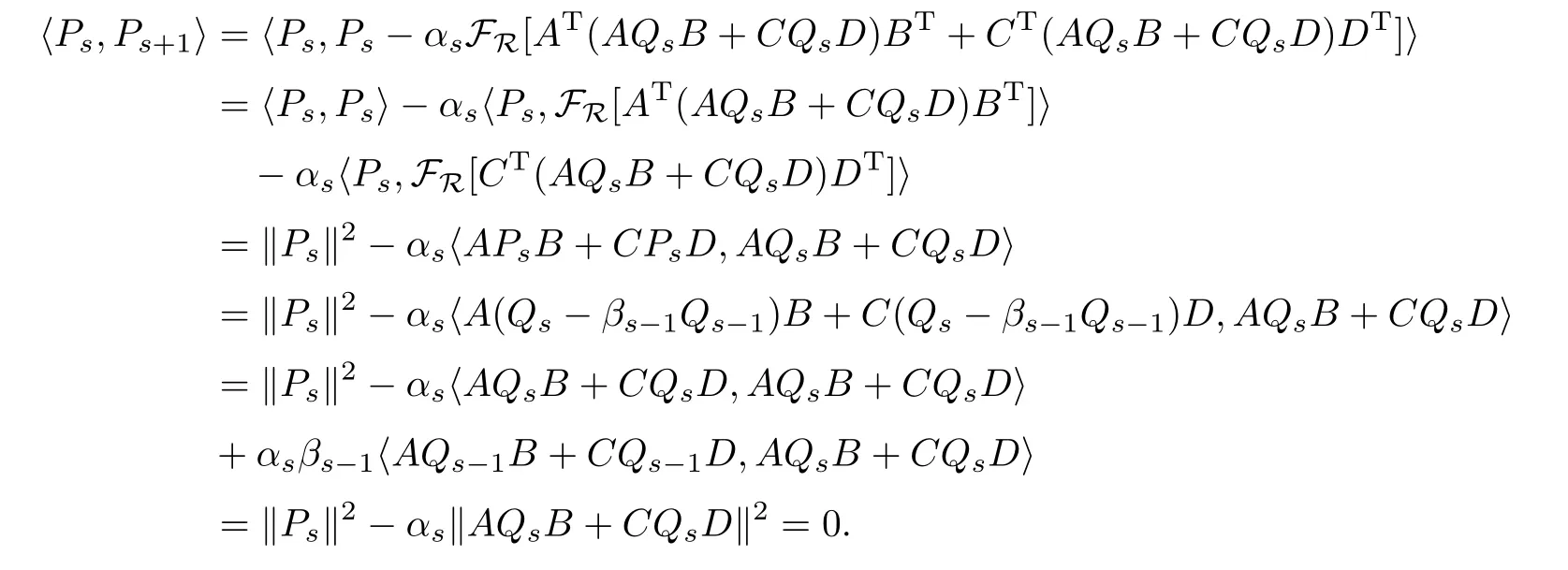
由算法I,與(5)式相類似的證明可得到

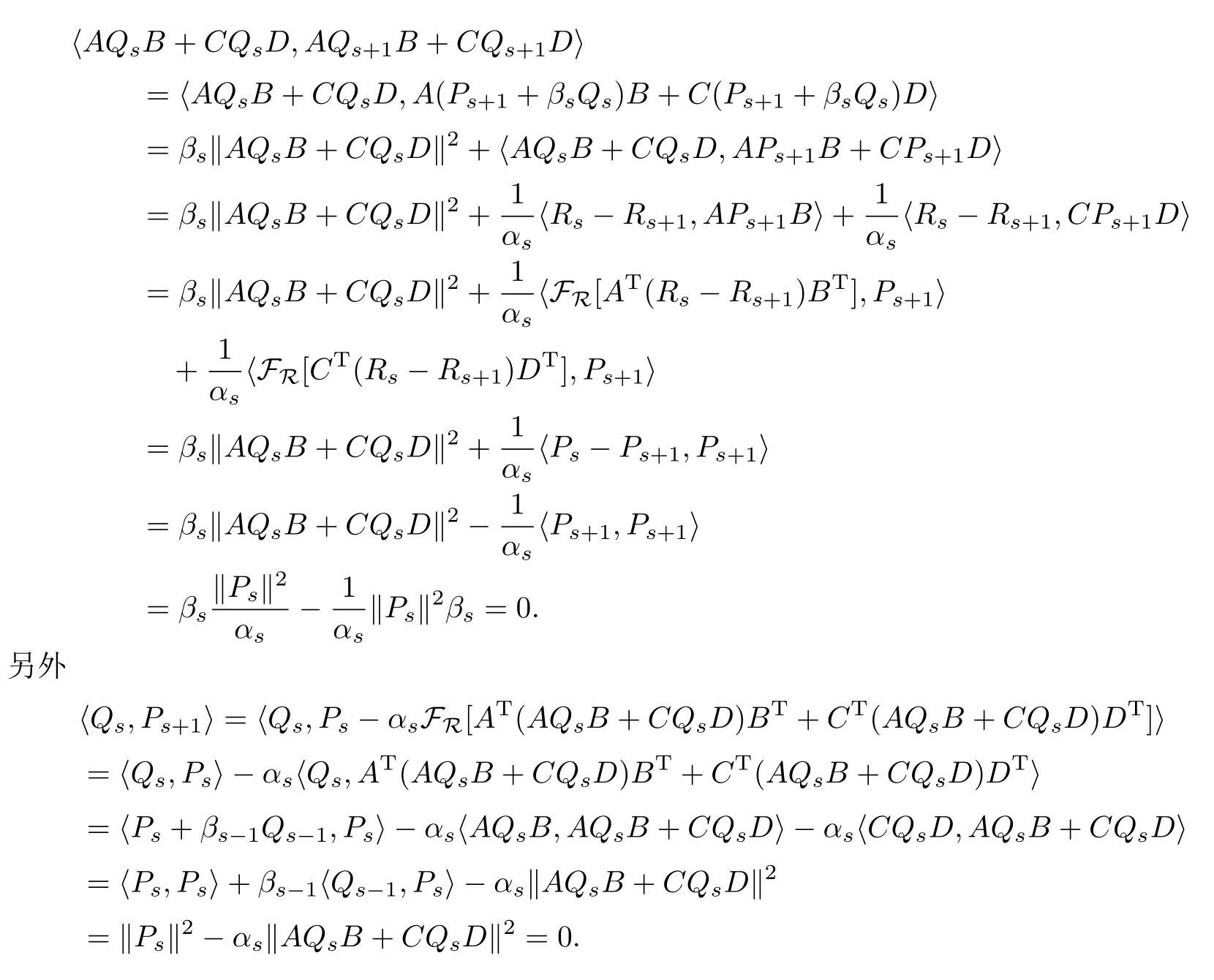
對i=1,2,3,···,s-1,注意到

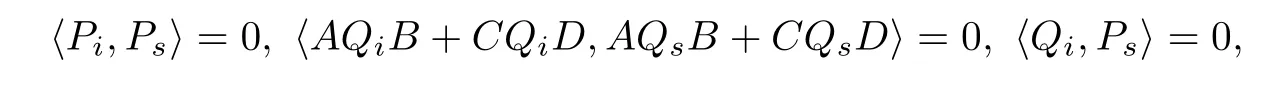
由算法I得到

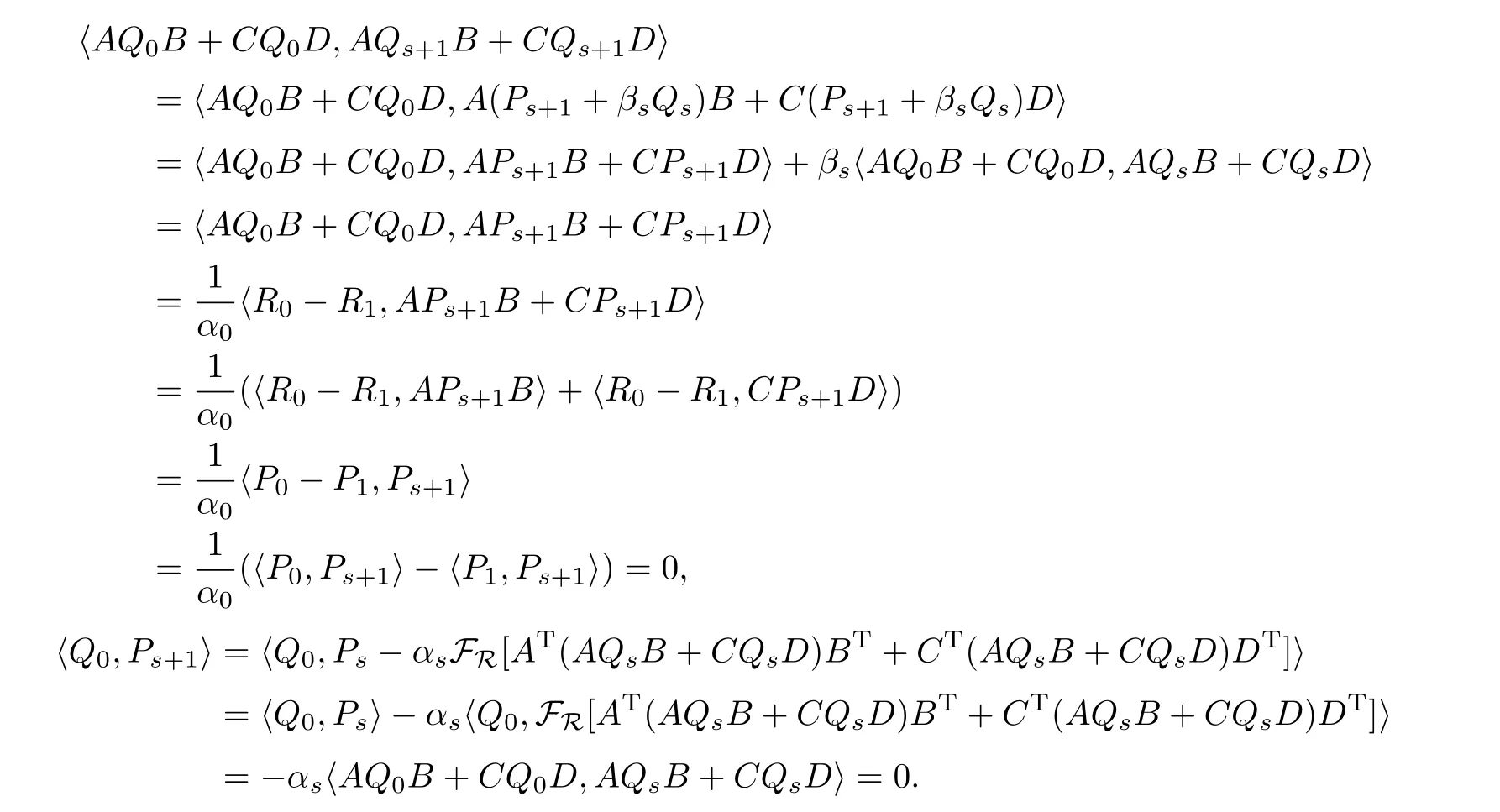
因此對t=s+1(3)式成立.

由數(shù)學(xué)歸納法知,引理2.3得到了證明.

注引理2.3中,若算法I在第k步迭代尚未停止,則意味著當(dāng)i=0,1,2,···,k時(shí),有Pi0,從而αi0且AQiB+CQiD0.下面予以說明.

若AQiB+CQiD=0,則

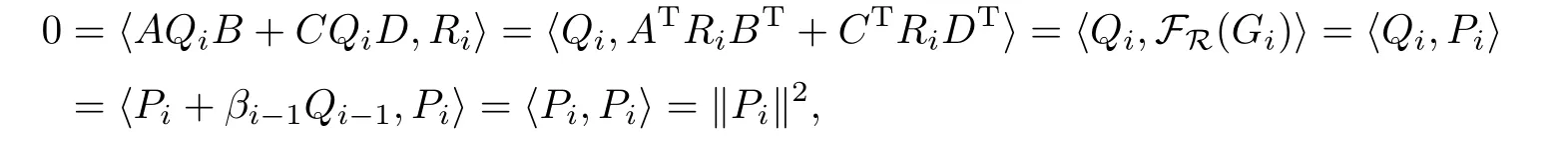
從而有Pi=0,故AQiB+CQiD0.

引理2.3表明,由算法I產(chǎn)生的矩陣序列P0,P1,P2···在矩陣空間R上是相互正交的,從而必定存在一個(gè)正整數(shù)r ≤st,使得Pr=0,從而得到下面的定理.

定理2.1在不考慮舍入誤差的情況下,對任意給定的初始矩陣X0∈R,算法I可在有限步內(nèi)計(jì)算出問題I的解.

引 理2.4若是問題I的解,則問題I的任意解均可表示為,其中X∈R且滿足AXB+CXD=0.

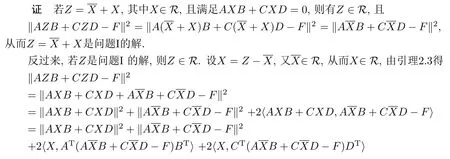
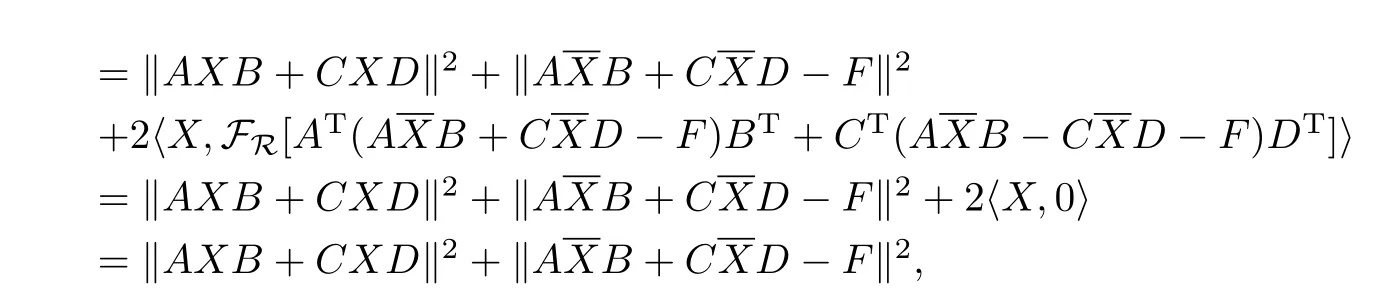
從而‖AXB+CXD‖2=0,即AXB+CXD=0.

定理2.2若取初始迭代矩陣X0∈FR(ATHBT+CTHDT),其中H是Rm×n中的任意矩陣,或者特別地,令X0=0s×t,則由算法I,通過有限步迭代可以得到問題I唯一的極小范數(shù)解.

證定義集合

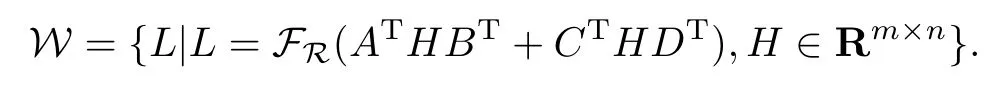
顯然W為線性子空間.若令初始迭代矩陣X0∈W,則由算法I得到的迭代更新矩陣Xk∈W.(k=1,2,···) 由算法I和定理2.1知,經(jīng)有限步迭代可得到問題I的解X*,且X*∈W.即存在H*∈Rm×n,使得X*=FR(ATH*BT+CTH*DT).

由引理2.4知,問題I的任意解可以表示為X*+X,其中X∈R,且滿足AXB+CXD=0.又

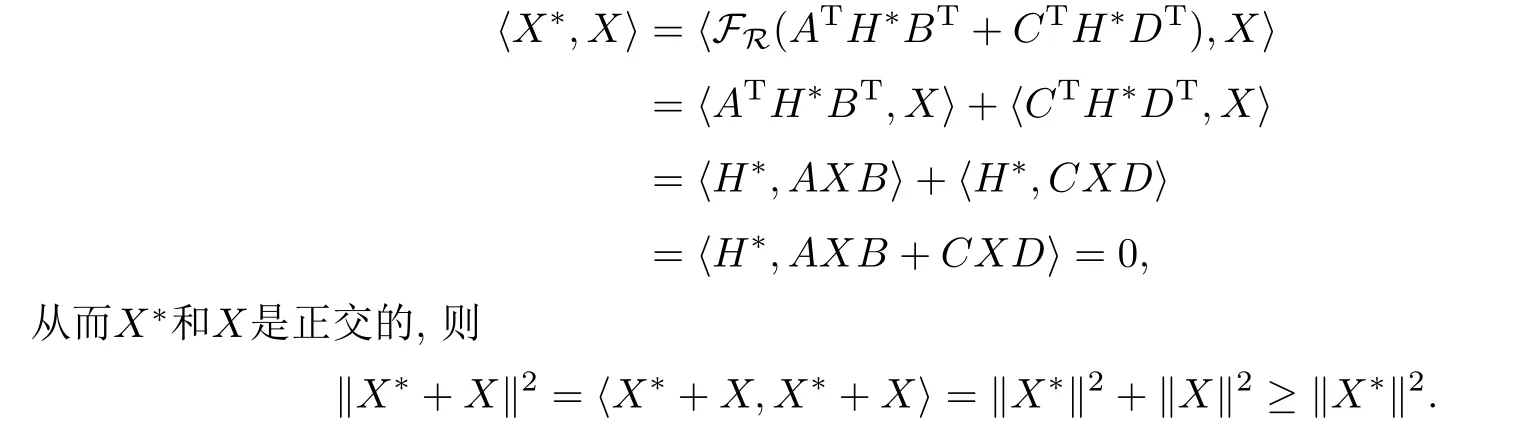
故X*為問題I的極小范數(shù)解.不難驗(yàn)證問題I的解集SE為非空閉凸集,其極小范數(shù)解存在且是唯一的.所以X*也是問題I的唯一極小范數(shù)解.

§3 問題II的解

因?yàn)閱栴}I的解集SE是非空閉凸集,故問題II的解存在且唯一.對問題II中給定的∈Rs×t,由于X∈R,因此

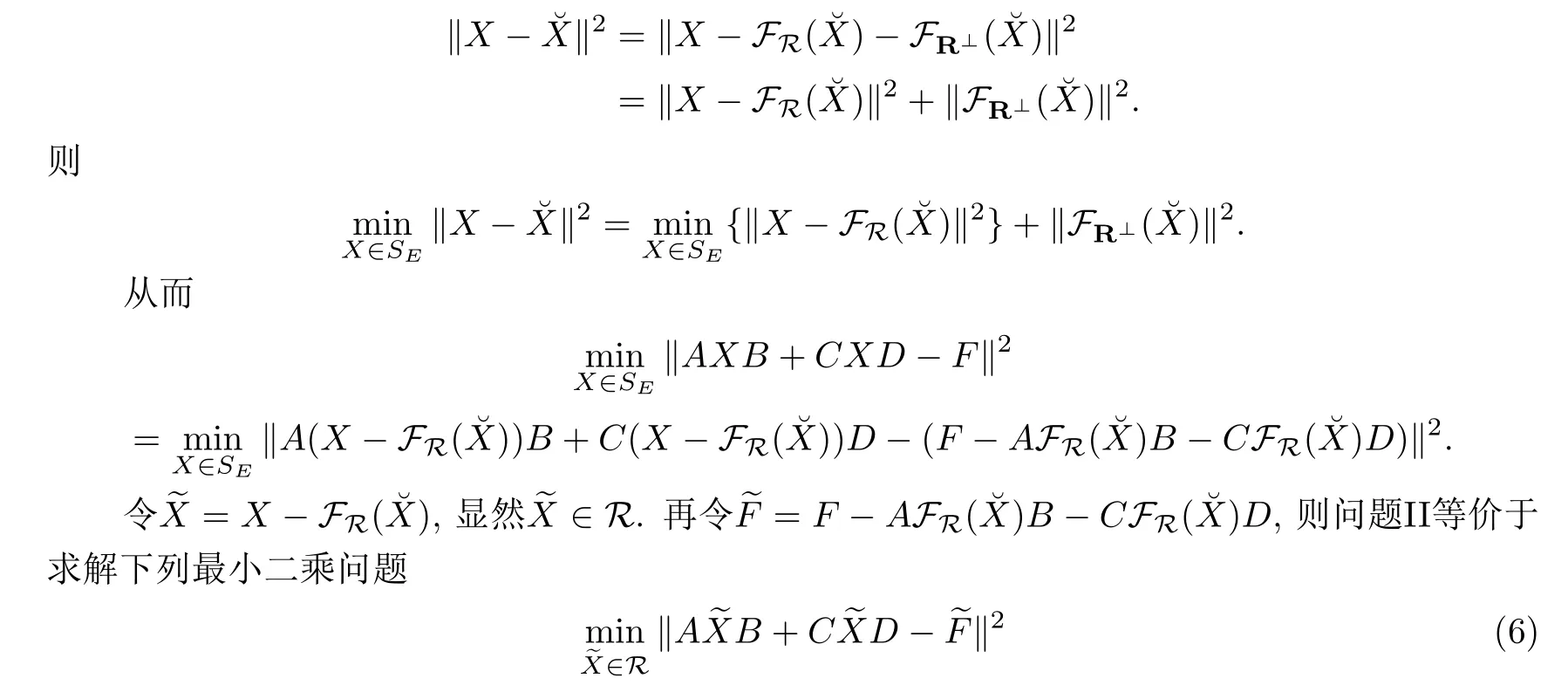
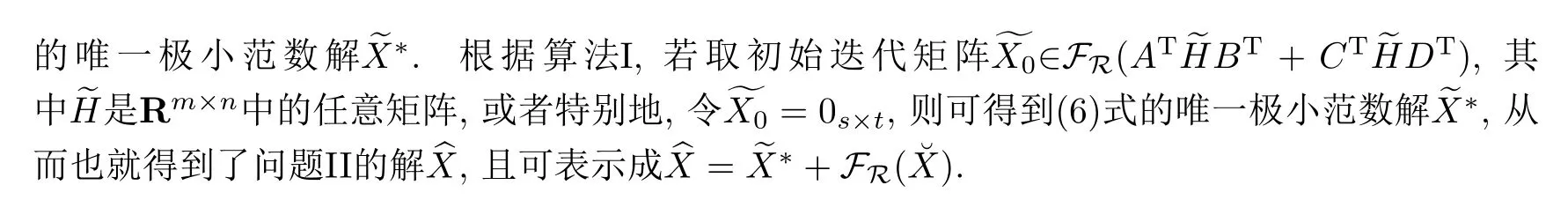
§4 數(shù)值例子

以下例子通過編寫M文件(見附錄solution.m)在Matlab R2017a(運(yùn)行環(huán)境: 64位Win7操作系統(tǒng),Intel(R) Core(TM) i3-2350M CPU @ 2.30GHz處理器,4.00GB內(nèi)存) 上運(yùn)行,所得結(jié)果證實(shí)了該算法的有效性.

例1在本例中將R取為n階實(shí)對稱矩陣集合,顯然,R為線性子空間.

在Rn×n上定義如下線性投影算子

由于計(jì)算誤差的影響,在具體的迭代過程中,Pi(i=0,1,2,···)一般不會等于零,迭代次數(shù)也不一定完全符合理論所需次數(shù).因此任取充分小的ε,譬如ε=1.0e-010(Matlab程序運(yùn)行結(jié)果中顯示,意思是1.0×10-10),當(dāng)‖Pk‖＜ε=1.0e-010時(shí),停止迭代,視Xk為問題I和問題II的解.

為了保持重復(fù)試驗(yàn)中結(jié)果的一致性,在Matlab中輸入隨機(jī)矩陣之前,需要將隨機(jī)發(fā)生器置于相同的初始狀態(tài).

(I) 不妨在Matlab中將隨機(jī)發(fā)生器置于狀態(tài)rand(’twister’,0),讓X0=rand(5)(注: rand(5)在Matlab中指的是各元素來自[0,1]區(qū)間且服從均勻分布的5階隨機(jī)矩陣).

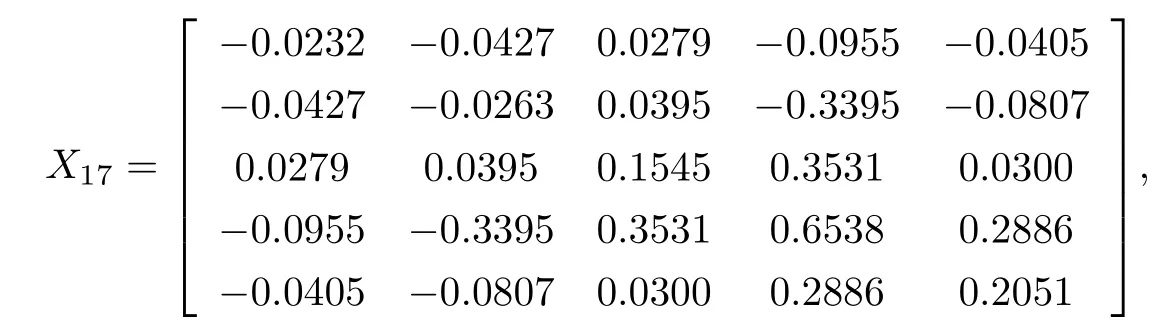
且‖P17‖=2.7559e-11＜ε,‖X17‖=1.0889,‖R17‖=14.9474,耗時(shí)t=0.0050秒.

若取初始迭代矩陣X0為5階零矩陣,經(jīng)過13(＜st=25)步迭代,得到問題I的唯一極小范數(shù)解

且‖P13‖=4.9355e-11＜ε,‖X13‖=0.3178,‖R13‖=14.9474,耗時(shí)t=0.0099秒.

在例1中,記迭代次數(shù)為k,定義r(k) :=log10‖Pk‖.下面圖1是r(k)與迭代次數(shù)k的變化曲線圖,它間接顯示了梯度投影矩陣范數(shù)‖Pk‖與迭代次數(shù)k的變化情況.

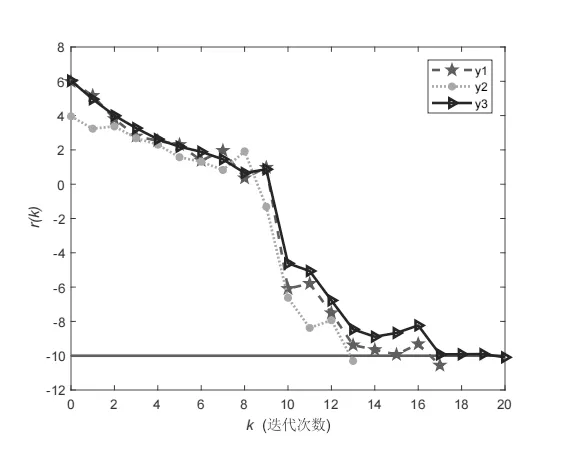
圖1 例1中r(k)曲線圖

圖1中,曲線y1和y2分別描述了求解問題I 時(shí),初始迭代矩陣X0分別為rand(5)和05×5時(shí)函數(shù)r(k)的變化情況,曲線y3描述了求解問題II 時(shí)函數(shù)r(k)的變化情況.圖1也顯示算法I在求解例1中的問題I和II時(shí)是可行的,有效的.

例2記R表示所有n階主對角線元素為零的矩陣構(gòu)成的集合.顯然R為線性子空間.

對任意的矩陣X=(xij)∈Rn×n,令

顯然X=X1+X2,且這樣的X1和X2唯一,又,故在Rn×n上定義線性投影算子

為了討論方便,不妨讓本例中的矩陣A,B,C,D,F,分別為例1中的矩陣,n=5.

(I) 在Matlab中將隨機(jī)發(fā)生器置于狀態(tài)rand(’twister’,0),不妨讓X0=rand(5),取初始迭代矩陣X0=X0-diag(diag(X0)),應(yīng)用算法I,經(jīng)過16(＜st=25) 步迭代,得到矩陣方程AXB+CXD=F在子空間R上的一個(gè)最小二乘解

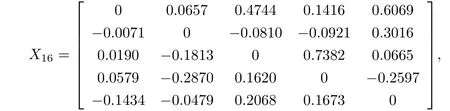
且‖P16‖=4.6810e-11＜ε,‖X16‖=1.2567,‖R16‖=14.9474,耗時(shí)t=0.0011秒.

若取初始迭代矩陣X0為5階零矩陣,經(jīng)過12(＜st=25) 步迭代,得到問題I的一個(gè)極小范數(shù)解

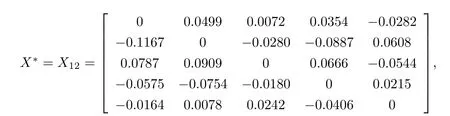
且‖P12‖=1.8840e-12＜ε,‖X12‖=0.2545,‖R12‖=14.9474,耗時(shí)t=0.0039秒.

顯然,X16∈R,X12∈R,‖X12‖＜‖X16‖,‖R16‖=‖R12‖.

在例2中,同樣地,定義r(k) :=log10‖Pk‖.下面圖2是r(k)與迭代次數(shù)k的變化曲線圖,它間接顯示了梯度投影矩陣范數(shù)‖Pk‖與迭代次數(shù)k的變化情況.

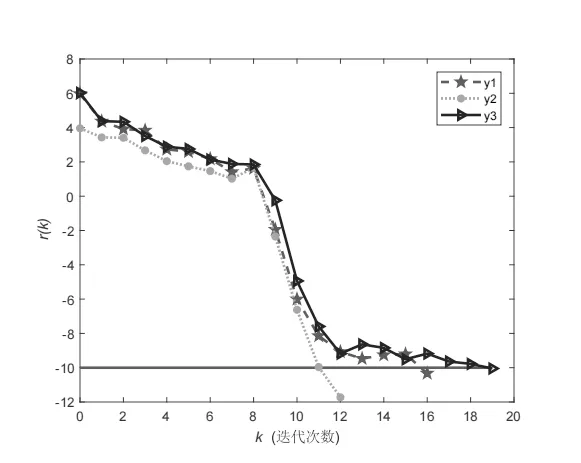
圖2 例2中r(k)曲線圖

圖2中曲線y1和y2分別描述了求解問題I時(shí),初始迭代矩陣X0分別為rand(5)和05×5時(shí)函數(shù)r(k)的變化情況,曲線y3描述了求解問題II時(shí)函數(shù)r(k)的變化情況.圖2也顯示算法I在求解例2中的問題I和II時(shí)是可行的,有效的.

§5 結(jié)論

應(yīng)用共軛梯度方法和線性投影算子,討論了矩陣方程AXB+CXD=F在任意線性子空間R約束下的最小二乘解問題.與最優(yōu)化中將負(fù)梯度在邊界上的投影作為迭代點(diǎn)前進(jìn)方向的梯度投影法不同的是,本文將矩陣函數(shù)的負(fù)梯度投影到所求線性子空間(矩陣空間)上的矩陣作為迭代過程中下一步的更新矩陣,以此來保證更新矩陣自動滿足線性子空間的約束.可以證明,在有限的誤差范圍內(nèi),所給算法經(jīng)過有限步迭代可得到矩陣方程AXB+CXD=F的最小二乘解,極小范數(shù)解及相應(yīng)的最佳逼近.最后分別以實(shí)對稱矩陣和主對角線元素為零的矩陣為對象進(jìn)行數(shù)值實(shí)驗(yàn),進(jìn)一步證實(shí)了算法的有效性.一般地,在Rs×t上定義線性投影算子F,就得到相應(yīng)的線性子空間R.因此,對于某線性子空間,只要定義相應(yīng)的線性投影算子,文中的迭代算法就可以用來求解矩陣方程AXB+CXD=F在該線性子空間約束下的最小二乘問題.

致謝審稿人提出的意見和建議極大地促進(jìn)了對原稿件的提升和完善,作者在此表示衷心的感謝.