跳躍數(shù)列探究
華東師范大學(xué)第二附屬中學(xué)(201203) 戴中元
單調(diào)性和周期性是數(shù)列的兩個(gè)重要性質(zhì),但也有很多數(shù)列既不單調(diào),也不是周期的,但它們也具有很好的規(guī)律,例如本文所要研究的“跳躍數(shù)列”,這種數(shù)列既具有一定的“單調(diào)性”,如我們可以知道連續(xù)三項(xiàng)之間的大小關(guān)系,又具有一定的“周期性”,如數(shù)列中的項(xiàng)可能在兩個(gè)數(shù)附近來回跳躍.
定義數(shù)列{an}從第三項(xiàng)開始,每一項(xiàng)都位于前兩項(xiàng)之間,我們稱它為跳躍數(shù)列.
根據(jù)定義可知,若數(shù)列{an}是跳躍數(shù)列,那么對(duì)任意連續(xù)三項(xiàng)ai,ai+1,ai+2,均有(ai-ai+2)(ai+2-ai+1)>0.
下面就以筆者于2020年上海市浦東新區(qū)第二次模擬考中所命的壓軸題為藍(lán)本來探討各種“跳躍數(shù)列”所具有的有趣性質(zhì).
問題1判斷下列兩個(gè)數(shù)列是否是跳躍數(shù)列:
①等差數(shù)列: 1,2,3,4,5,···;
根據(jù)定義易知①等差數(shù)列: 1,2,3,4,5,···不是跳躍數(shù)列; 由于等差數(shù)列的公差d >0 時(shí), 它是單調(diào)遞增數(shù)列;d <0 時(shí), 它是單調(diào)遞減數(shù)列;d=0 時(shí), 它是常數(shù)列, 所以等差數(shù)列不可能是跳躍數(shù)列.根據(jù)定義可知②等比數(shù)列:,···是跳躍數(shù)列.如果等比數(shù)列{an}是跳躍數(shù)列,那么
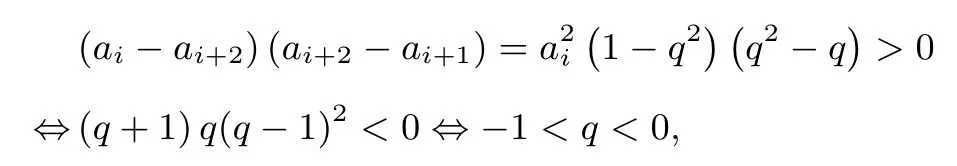
所以我們可以得到
命題1等比數(shù)列是跳躍數(shù)列的充要條件是公比q ∈(-1,0).
為更加直觀地理解跳躍數(shù)列的變化情況, 我們利用蛛網(wǎng)圖來表示{an}, 設(shè)an+1=f(an), 作函數(shù)f(x)和y=x的圖像.先在y=x上取點(diǎn)A1(a1,a1), 過A1作平行于y軸的直線交f(x)的圖像于B1(a1,a2), 再過B1作平行于x軸的直線交y=x于A2(a2,a2), 依次類推可得A2,B2,A3,B3,···,這樣就可以得到數(shù)列{an}的蛛網(wǎng)圖,這里An的橫坐標(biāo)和縱坐標(biāo)即為an.通過蛛網(wǎng)圖我們可以研究數(shù)列{an}的各種性質(zhì),例如單調(diào)性和周期性.
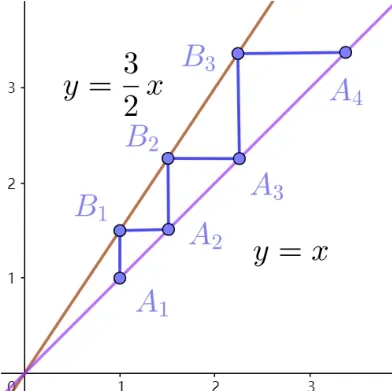
圖1
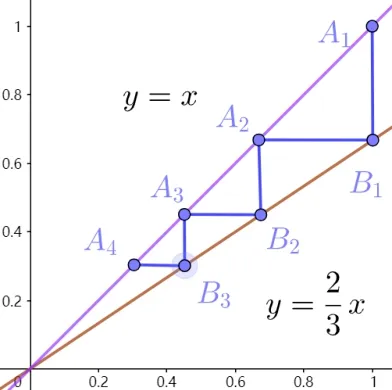
圖2
如圖3 中f(x)=1-|2x-1|(x ∈[0,1],稱為帳篷函數(shù)),可以看到A4與A1重合,所以{an}是周期為3的周期數(shù)列.
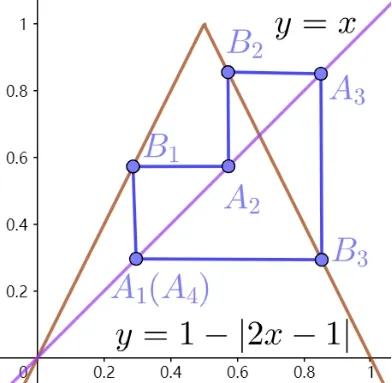
圖3
從蛛網(wǎng)圖可知,{an}是跳躍數(shù)列等價(jià)于An+2始終在An,An+1這兩點(diǎn)間.如圖4 中可知符合跳躍數(shù)列的等價(jià)條件.
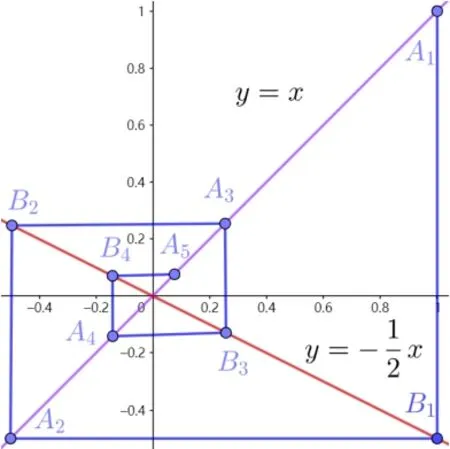
圖4
命題2已知{an}滿足: 對(duì)任何正整數(shù)n, 均有an+1=(a1>0).則數(shù)列{an}是跳躍數(shù)列的充分必要條件是0<a1<1.
證明(1)必要性: 若a1>1,則{an}是單調(diào)遞增數(shù)列,不是跳躍數(shù)列;若a1=1,{an}是常數(shù)列,不是跳躍數(shù)列.
(2)充分性: 下面用數(shù)學(xué)歸納法證明: 若0<a1<1,則對(duì)任何正整數(shù)n,均有a2n-1<a2n+1<a2n,a2n >a2n+2>a2n+1成立.
(2.1)當(dāng)n=1 時(shí),a2==a1,a3==a2, 因?yàn)閍2=1,所以a3==a1,所以a2>a3>a1,因?yàn)閍2>a3>a1,所以3<a4<a2,所以n=1 命題成立.
(2.2)若n=k時(shí),a2k-1<a2k+1<a2k,a2k >a2k+2>a2k+1, 則aa2k <aa2k+2<aa2k+1,所以a2k+1<a2k+3<a2k+2,aa2k+1>aa2k+3>aa2k+2,所以a2k+2>a2k+4>a2k+3,所以當(dāng)n=k+1 時(shí)命題也成立.
根據(jù)數(shù)學(xué)歸納法, 可知命題成立, 數(shù)列滿足(ai-ai+2)(ai+2-ai+1)>0,故{an}是跳躍數(shù)列.
例如當(dāng)a1=0.5 時(shí),an+1=f(an),其中f(x)=0.5x,圖5 表示的即為迭代過程A1(a1,a1)→B1(a1,a2)→A2(a2,a2)→B2(a2,a3)→A3(a3,a3)→B3(a3,a4)→···,其中A3在A1,A2之間,A4在A2,A3之間,A5在A3,A4之間,符合{an}是跳躍數(shù)列的等價(jià)條件.bn+1∈(-∞,-1)∪(2,+∞),若bn ∈(-∞,-1)∪(2,+∞),則bn+1∈(-1,2).

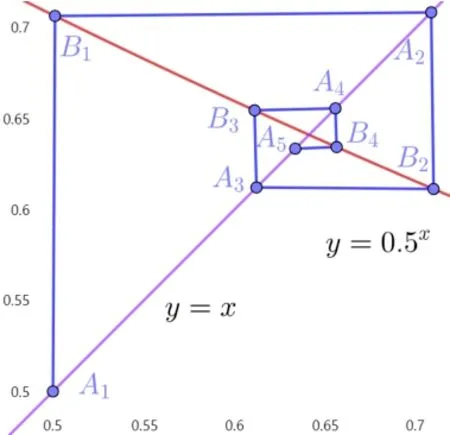
圖5
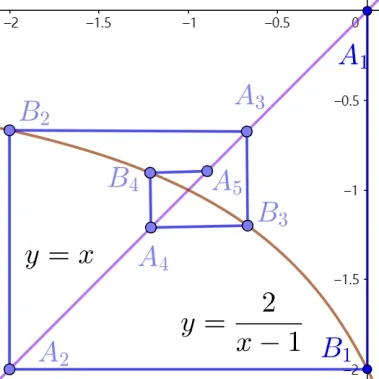
圖6

綜上,b1∈(-∞,-1)∪(-1,1).其他分式線性遞推數(shù)列也可類似討論.
問題3跳躍數(shù)列{cn}滿足對(duì)任意正整數(shù)n均有,求首項(xiàng)c1的取值范圍.
解本題難點(diǎn)在于如何化簡(jiǎn)(cn+2-cn+1)(cn+2-cn),這里給出兩種思路.
思路1(利用平方差公式)
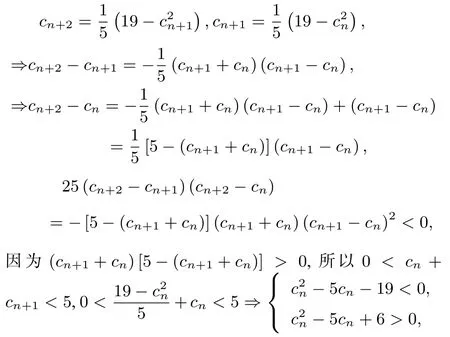


在上例中如令c1=如圖7 可見{cn}是跳躍數(shù)列, 并且始終在兩個(gè)區(qū)間之間來回跳躍, 其中奇數(shù)項(xiàng)單調(diào)遞減趨近于3, 而偶數(shù)項(xiàng)單調(diào)遞增趨近于2,所以這里蛛網(wǎng)圖不斷地趨向于以(2,2),(2,3),(3,2),(3,3)為頂點(diǎn)的正方形.這里2 和3 是f(x)的周期為2 的點(diǎn), 即滿足f(f(x))=x,也可把它稱為f(x)的穩(wěn)定點(diǎn)(不動(dòng)點(diǎn)可以視作周期為1 的點(diǎn)),所以在這里這個(gè)跳躍數(shù)列的性質(zhì)和周期性是緊密相連的.
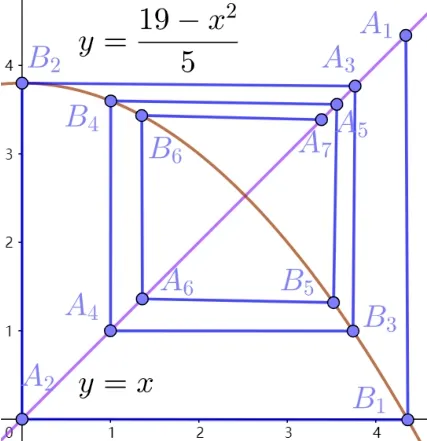
圖7

