Mathematical Reflections 的S357 號(hào)問(wèn)題的加強(qiáng)

福建師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院 楊標(biāo)桂（郵編：330117）

關(guān)鍵字 外接圓半徑; 內(nèi)切圓半徑; 高線

1 問(wèn)題提出

蒂圖·安德雷斯庫(kù)[1]的Mathematical Reflections (2014-2015)中提供了如下幾何不等式:

Mathematical Reflections S357問(wèn)題在任意△ABC的中,BC=a,CA=b,AB=c,ha,hb,hc分別為對(duì)應(yīng)邊上的高,r為△ABC的內(nèi)切圓半徑, 則有:

定理1 在任意△ABC的中,BC=a,CA=b,AB=c,ha,hb,hc分別為對(duì)應(yīng)邊上的高,r為△ABC的內(nèi)切圓半徑, 則有

于是②可以推出①.

更一般地, 我們有:

定理2 在任意△ABC的中,BC=a,CA=b,AB=c,ha,hb,hc分別為對(duì)應(yīng)邊上的高,R,r分別為△ABC的外接圓半徑與內(nèi)切圓半徑, 則有

由定理2 的③式和Euler 不等式可知定理1成立.

2 幾個(gè)引理

為了證明定理2, 我們先建立一個(gè)關(guān)于高與內(nèi)切半圓徑的恒等式, 即不等式②的最佳形式:

引理1 在任意△ABC的中,BC=a,CA=b,AB=c,ha,hb,hc分別為對(duì)應(yīng)邊上的高,R,r,s分別為△ABC的外接圓半徑、內(nèi)切圓半徑和半周長(zhǎng), 則有

利用熟知的恒等式∑a=2s;∑bc=s2+r2+4Rr;∏a=abc=4Rrs(其中∏ 表示循環(huán)積), 經(jīng)計(jì)算可得

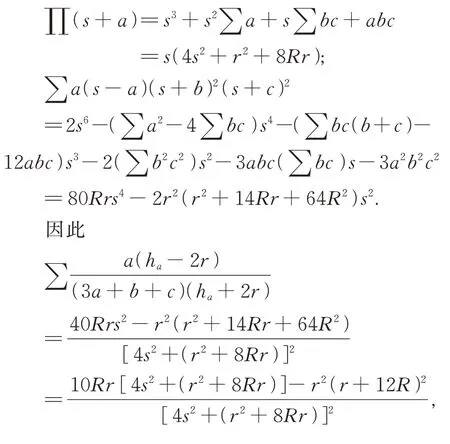
于是引理1 獲證.

其次, 我們引入著名的Gerretsen 不等式:

引理2 (Gerretsen 不等式) 設(shè)R,r,s分別是△ABC的外接圓半徑, 內(nèi)切圓半徑與半周長(zhǎng), 則有

16Rr-5r2≤s2≤4R2+4Rr+3r2⑥

3 定理2 的證明

下面利用恒等式⑤與Gerretsen 不等式⑥證明定理2:

定理2 得證.