廣東省中山市中山紀念中學(528454) 李文東

設n個小杯中依次盛有b1,b2,···,bn克糖水,并且分別含糖a1,a2,···,an克.

其中(2)(3)稱為糖水不等式(我們分別稱為糖水不等式1 和2,下文不再說明),恰當運用這些不等式,能給解題帶來很大的方便,下面舉例說明.

一.利用糖水不等式比較大小

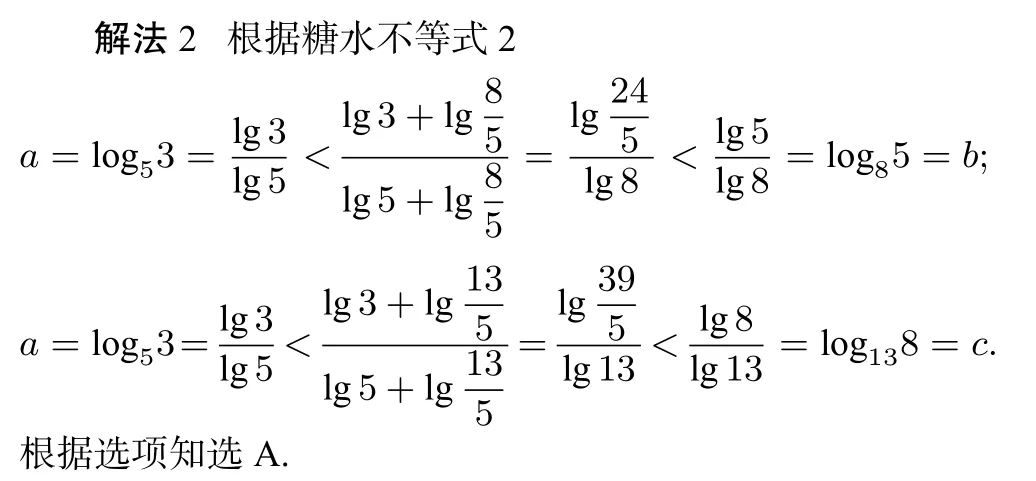
點評原題給出條件55<84,134<85,在我們用了糖水不等式后,該條件就可以去掉,當然如果要比較b,c的大小,僅用糖水不等式是不夠的:

點評將對數(shù)用換底公式改寫成真分數(shù)的形式,然后利用糖水不等式和對數(shù)的運算法則將需要比較的兩個對數(shù)的分母或分子化為相同來比較大小.

二.利用糖水不等式解決函數(shù)單調性問題

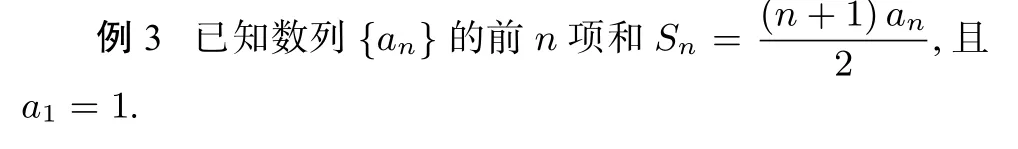
(1)求數(shù)列{an}的通項公式;

(2)令bn=lnan,是否存在k(k≥2,k ∈N?),使得bk、bk+1、bk+2成等比數(shù)列.若存在,求出所有符合條件的k值;若不存在,請說明理由.

三.利用糖水不等式處理數(shù)列不等式問題

例4(2014 高考全國II 卷第17 題)已知數(shù)列{an}滿足a1=1,an+1=3an+1.

這類乘積型的不等式在高考題中經(jīng)常出現(xiàn),比如2009廣東理科高考題:

已知曲線Cn:x2?2nx+y2=0(n=1,2,···).從點P(?1,0)向曲線Cn引斜率為kn(kn >0)的切線ln,切點為Pn(xn,yn).

(1)求數(shù)列{xn}與{yn}的通項公式;

波利亞曾指出:“好問題同某種蘑菇有些相像,它們都成堆地生長,找到一個以后,你應當在周圍找找,很可能附近就有好幾個.”利用這種手法,還可以得到一連串的不等式群,讀者不妨一試!

例6求證: 當n≥2,n ∈N?時

從上述問題看到,對于涉及到分式的大小或不等式問題,可以觀察所給分式的特征,考慮利用糖水不等式進行適當放縮來處理,這往往能夠達到意想不到的效果!