廣東省東莞市第八高級(jí)中學(xué)(523629) 何國(guó)鋒

1 問題提出

人教版選擇性必修第一冊(cè)在“1.4.2 用空間向量研究距離、夾角問題”[1]中借助投影向量給出了空間內(nèi)點(diǎn)P到直線l的距離公式:

√

(v為直線的方向向量,v0為直線的單位方向向量,A為直線上一點(diǎn))以及點(diǎn)P到平面α的距離公式:

(n為平面的法向量,n0為平面的單位法向量,A為平面α內(nèi)一點(diǎn)).

教材關(guān)于兩個(gè)公式推導(dǎo)方式: 公式1○用到了的是向量在直線方向向量v上的投影向量以及勾股定理; 公式2○用到了的是向量在平面的法向量n上的投影向量,這么處理充分發(fā)揮了向量的工具作用,巧妙的利用了投影向量,學(xué)生也比較容易理解和接受. 但從公式的結(jié)構(gòu)上來看公式1○顯然比較復(fù)雜,不是十分美觀,學(xué)生也不便于記憶. 筆者的思考是: (1)教材為什么采用在不同的向量上的投影向量來處理呢? (2)這兩個(gè)公式能否統(tǒng)一,使得公式更加簡(jiǎn)潔美觀呢?

2 問題解決

首先,要統(tǒng)一我們必須給出一個(gè)與直線垂直的向量,我們可以類比平面的法向量定義,來定義直線的法向量:

定義設(shè)直線l在平面α內(nèi),我們把所在直線垂直于l且平行于平面α(或在α內(nèi))的非零向量n稱為直線l在平面α內(nèi)法向量(如圖一所示).

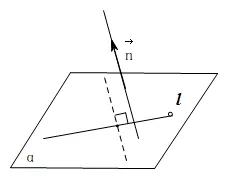
圖1

如圖2, 設(shè)點(diǎn)P與直線l(P在l外) 所確定的平面為α, 已知直線在平面內(nèi)的法向量為n,A為直線l上一點(diǎn), 則P到l的距離為在n上的投影向量的長(zhǎng)度即

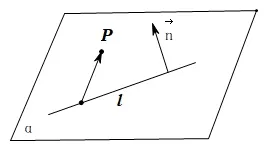
圖2

由此,借助直線的法向量以及平面的法向量我們可以將兩個(gè)公式1○2○統(tǒng)一為:

其中: (1)當(dāng)是點(diǎn)到直線線距離時(shí),設(shè)l與點(diǎn)確定的平面為α,n為l在平面α內(nèi)法向量;A為直線上一點(diǎn);

當(dāng)是點(diǎn)到平面距離時(shí),n為平面的法向量;A為平面內(nèi)一點(diǎn).

接下來,我們?nèi)绻霉?○來求點(diǎn)到直線的距離,必須解決的問題如何求直線l在平面α內(nèi)的法向量呢? ,在此提供如下兩個(gè)方法:

方法1: 如圖3,設(shè)l與點(diǎn)P確定的平面為α,其中α法向量為m,直線l的方向向量為v,所求直線的法向量為n,則利用n ⊥m,n ⊥v即可求出一個(gè)直線l在平面α內(nèi)法向量.

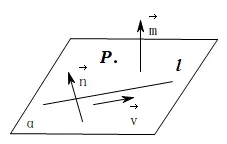
圖3

方法2: 如圖4,設(shè)l與點(diǎn)P確定的平面為α,向量a,b為α內(nèi)不共線的向量,所求直線的法向量為n,根據(jù)向量共面定理,存在實(shí)數(shù)x,y,使得n=xa+yb,最后利用n ⊥v(v為直線方向向量)即可求出一個(gè)直線l在平面α內(nèi)法向量.

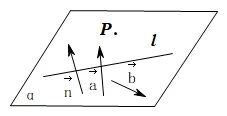
圖4

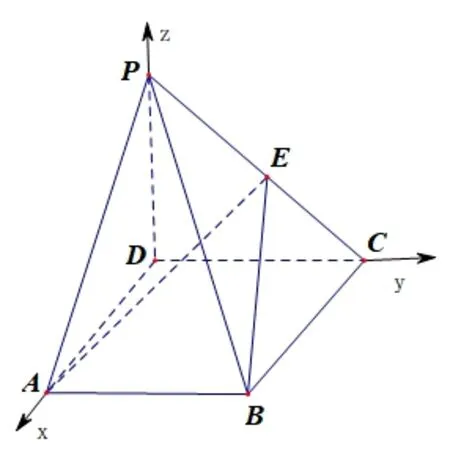
圖5

3 應(yīng)用舉例

例題1在四棱錐P -ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC=2,E是PC的中點(diǎn),求A到BE的距離.

通過以上分析與應(yīng)用,我們將兩種距離公式在結(jié)構(gòu)上進(jìn)行了統(tǒng)一,使得公式更加美觀,學(xué)生也更加便于記憶和運(yùn)用,同時(shí)推導(dǎo)過程使學(xué)生對(duì)距離的本質(zhì)的理解以及向量在幾何中的作用影響更為深刻. 不僅如此,如果將公式運(yùn)用平面解析幾何中點(diǎn)到直線距離公式的推導(dǎo)過程中,就可以避免教材推導(dǎo)過程[2]中的復(fù)雜計(jì)算, 可以節(jié)約時(shí)間也便與學(xué)生記憶,還可以進(jìn)一步讓學(xué)生體會(huì)到數(shù)學(xué)的和諧和統(tǒng)一美[3].

例題2(推導(dǎo)平面內(nèi)點(diǎn)到直線的距離公式) 設(shè)直線l:Ax+By+C=0,點(diǎn)P(x0,y0),求P到直線l的距離.

解: 如圖6, 易知l的方向向量V= (B,-A), 設(shè)其法向量為n= (x,y), 由n ⊥ v得,Bx -Ay= 0, 令x=A, 則y=B, 即n= (A,B). 設(shè)Q(x1,y1) 為直線上一點(diǎn), 則Ax1+By1+C= 0,= (x0-x1,y0-y1), 從而,· n=A(x0-x1) +

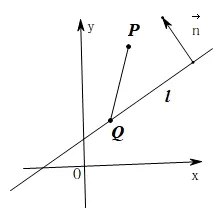
圖6