許愛(ài)瑛 (陜西省咸陽(yáng)中學(xué) 712000)

2020年馬其頓數(shù)學(xué)奧林匹克競(jìng)賽中有一道不等式證明題:

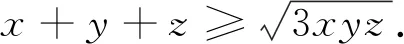
文[1]用三角換元法給出了證明,但證明過(guò)程比較復(fù)雜.如果注意到不等式①兩邊的結(jié)構(gòu),聯(lián)想到均值不等式,則可獲得一種十分簡(jiǎn)單的證明．

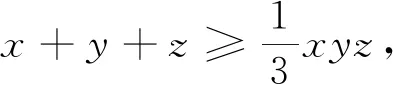
將問(wèn)題1推廣,得到下列結(jié)論:

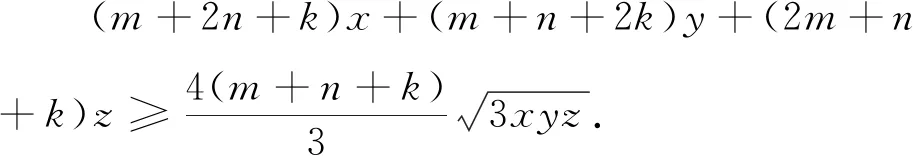
證明 由已知條件及均值不等式,得

9(m+n+k)=mxy+nyz+kzx≥

解得xk+mym+nzn+k≤32(m+n+k),所以

(m+2n+k)x+(m+n+2k)y+(2m+n+k)z

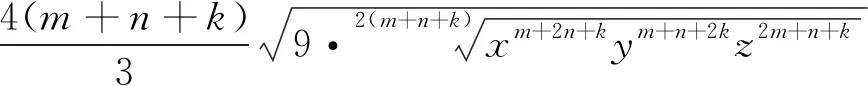
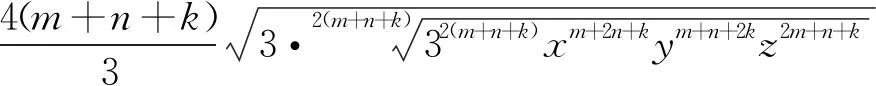
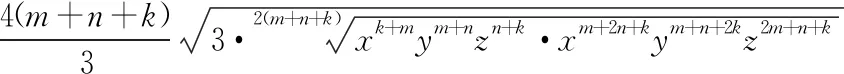
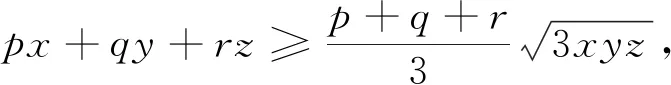
如果將推廣1及其證明中的3換為正實(shí)數(shù)p,那么類(lèi)似地可以證明:

推廣2正實(shí)數(shù)x,y,z,p及正整數(shù)m,n,k滿(mǎn)足mxy+nyz+kzx=p2(m+n+k),求證:(m+2n+k)x+(m+n+2k)y+(2m+n+k)z≥

如果考慮將問(wèn)題1的已知條件和所證不等式互換位置,那么可以得到如下逆命題:

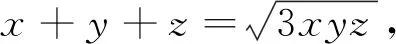
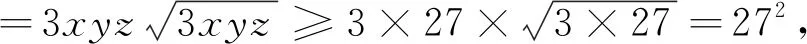
將問(wèn)題2推廣,得到下列結(jié)論:

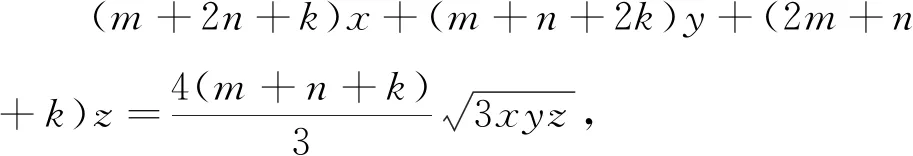
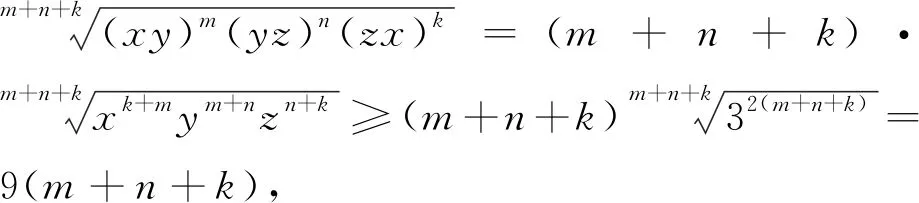
類(lèi)似地,可以證明:

上面對(duì)競(jìng)賽題及其逆命題的推廣,只是將已知條件和要證明的不等式中變量的系數(shù)進(jìn)行了拓展,但不等式等號(hào)成立的條件仍然是x=y=z,對(duì)于其他取等號(hào)的條件,不等式會(huì)怎樣變化呢?留給有興趣的讀者去思考吧．