鄭仕福

? 福建省廈門市集美中學

解題教學是高中數(shù)學教學的基本活動形式,通過解題可以培養(yǎng)學生數(shù)學核心素養(yǎng)和思維能力.問題鏈教學以問題為基礎引導學生思考、分析問題,掌握解題思路,幫助他們掌握知識并培養(yǎng)解題能力.

1 高中數(shù)學項目化解題教學問題鏈設計

基于問題鏈的高中數(shù)學項目化解題教學以問題為導向,讓學生通過思考和求解問題來提升解題能力.因此需要按照表1中的解題教學原則來設計問題鏈,培養(yǎng)學生的解題能力.

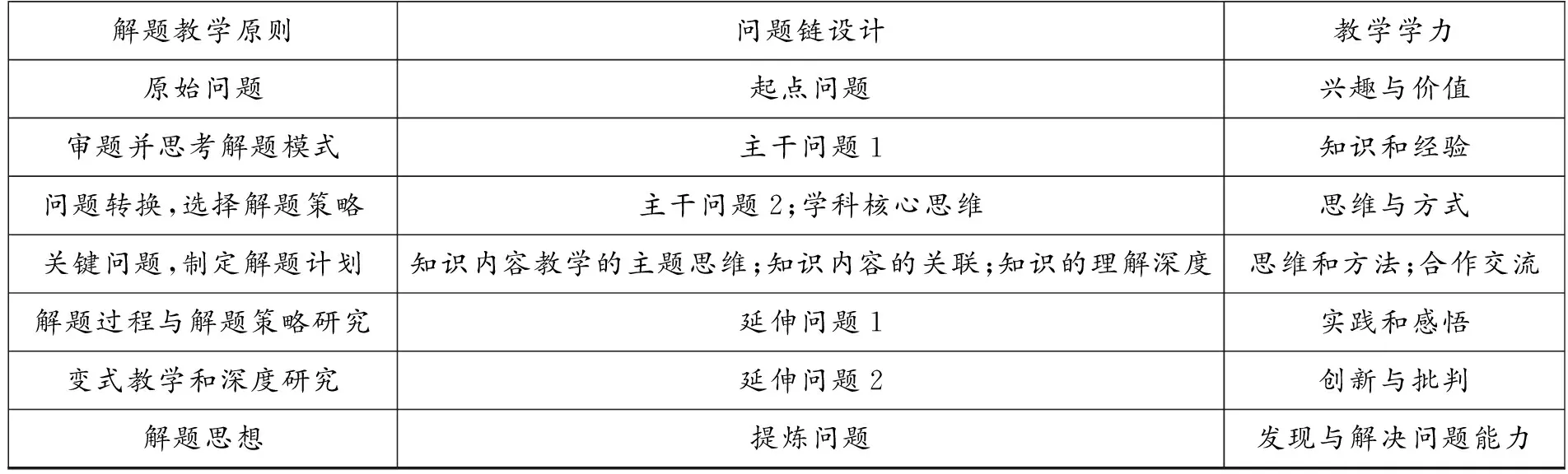
表1 高中數(shù)學項目化解題教學原則和問題鏈設計

2 基于問題鏈的高中平面向量項目化解題教學

2.1 原題呈現(xiàn)

A.[-5,3] B.[-3,5]

C.[-6,4] D.[-4,6]

2.2 主干問題

問題1題目中給定了哪些幾何關系?

審題時,首先要明確題目中所給定的已知條件,根據已知條件進行相關關系的確定.本題中所給定的已知條件是在△ABC中,AC=3,BC=4,∠C=90°,P為△ABC所在平面內的一動點,且PC=1,由已知條件可以確定△ABC是以AB為斜邊的直角三角形,同時知道兩條直角邊的長度分別是AC=3,BC=4,并且能夠確定點P的運動軌跡是以C為圓心,半徑為1的圓[1].

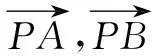
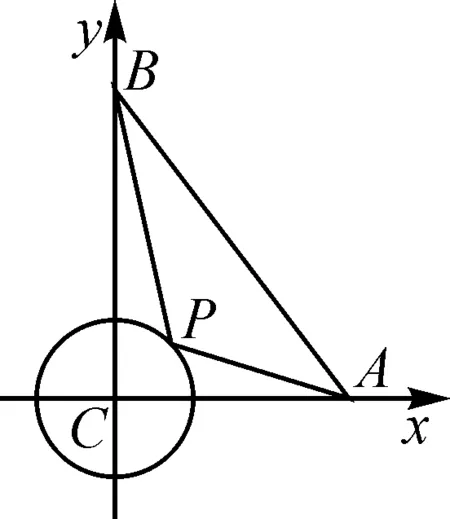
圖1

表示向量就需要將幾何關系進行代數(shù)化轉換,所以需要建立平面直角坐標系,利用幾何關系構建如圖1所示的平面直角坐標系.根據幾何位置關系確定點的坐標,即A(3,0),B(0,4),進而利用點的坐標來表示向量.

問題2-2點P的坐標如何表示?

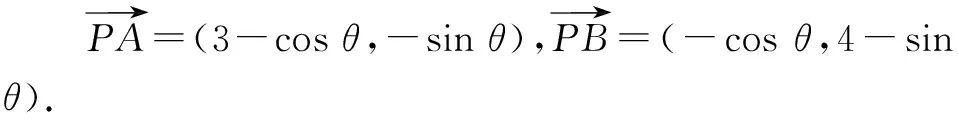
評析：這種解題思路是通過建立平面直角坐標系,充分利用PC=1,利用三角函數(shù)將點P的坐標表示為P(cosθ,sinθ),再表示出向量,最后利用三角函數(shù)的定義域來確定取值范圍.

2.3 延伸問題

問題3本題由于PC=1,通過上述解題方式求解不會存在較大的計算問題,但是如果PC的值是變化的,就會增加本題的難度.是否存在一種解題思路,使運算過程不會因PC值的變化而受到太大的影響?

解法1：利用極化恒等式求解.

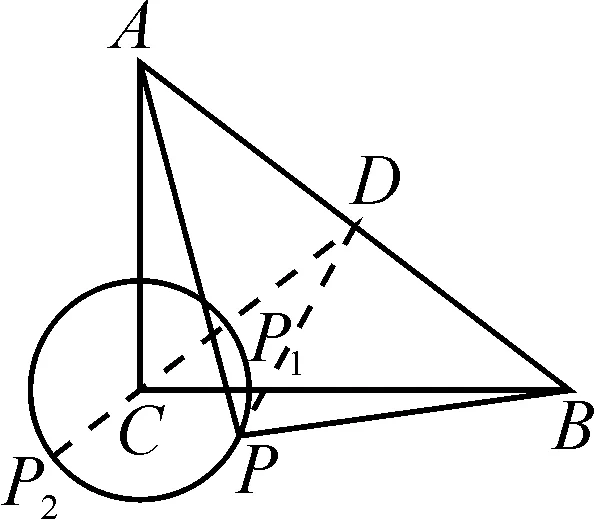
圖2

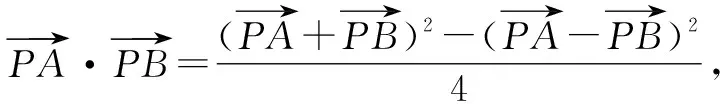
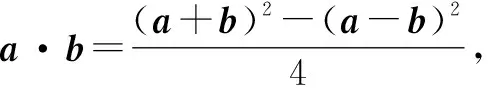
解法2：利用解析幾何方式求解.

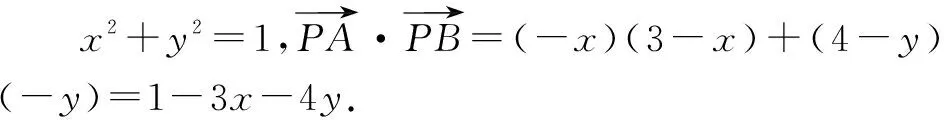
2.4 提煉問題

問題4結合上述三種解題策略,總結平面向量的一般解題策略(如圖3).

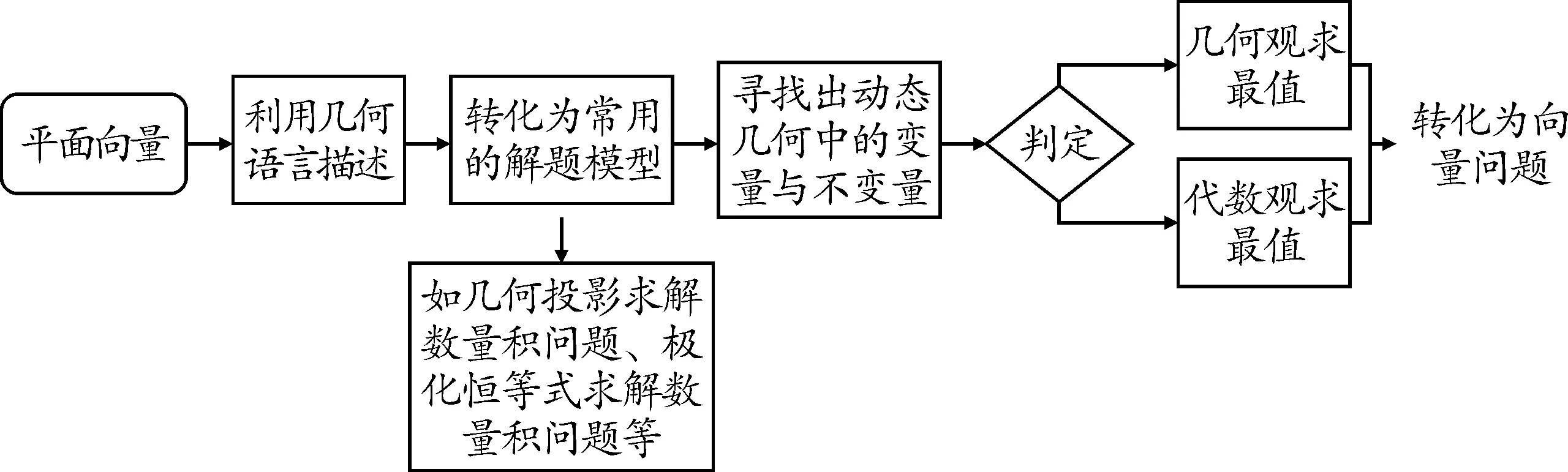
圖3 平面向量問題解題策略

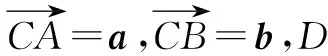
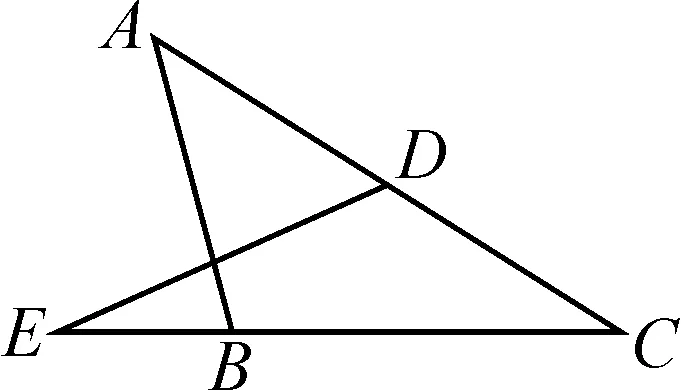
圖4

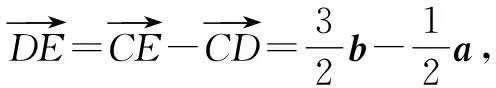
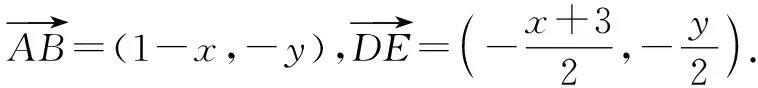
評析：本題是以平面向量的一般解題策略來求解的.通過幾何描述表示題目中已知的條件,從而確定題目所展示的幾何關系,判斷位置關系,進而設計解題策略實現(xiàn)問題的求解.

3 教學反思

平面向量問題涉及學生的數(shù)學思維和學科素養(yǎng).首先,可以考查學生的直觀想象能力,通過幾何圖形展示問題并根據圖形特征選擇解題策略.其次,可以考查學生的邏輯推理能力,如對極化恒等式進行演繹推理.最后,可以考查學生的數(shù)學運算能力,因為運算錯誤可能導致結果錯誤.解題教學應該回歸數(shù)學的本質和通用方法.在平面向量問題中,解析法和基底法是常用的解題方法,而極化恒等式是一種特別的向量分解方法[5].這些方法是解決平面向量問題的關鍵.高中數(shù)學項目化解題教學應該回歸數(shù)學的本質,并結合實際問題尋找解題的一般策略.通過分析主干問題來找到解題的突破口,然后結合延伸問題確定解題策略,實現(xiàn)問題的求解.平面向量問題的解題一般策略可以有效解決相關問題.

綜上所述,平面向量問題的解題教學應該注重對學生數(shù)學思想和數(shù)學學科素養(yǎng)的培養(yǎng),采用合適的解題策略,回歸數(shù)學的本質和通性通法.結合實際問題尋找解題一般策略是高中數(shù)學項目化解題教學的關鍵.