殷峰麗

極限是研究數(shù)列和函數(shù)性質的重要工具,和式極限的求解是極限運算的一個重要組成部分.利用定積分的定義將所求的和式極限直接化成某個函數(shù)的積分和,是計算和式極限的一種有效方法,但是有些題目并不能直接轉化為某個函數(shù)的積分和.為此,本文利用無窮小分析法,從理論上說明可將所給題目中的被加項用等價無窮小來代替,然后再化為某個函數(shù)的積分和,進而有效地解決問題.

定理 設f(x),g(x)在[a,b]上可積,g(x)≠0,x∈(a,b),若,則

證 令

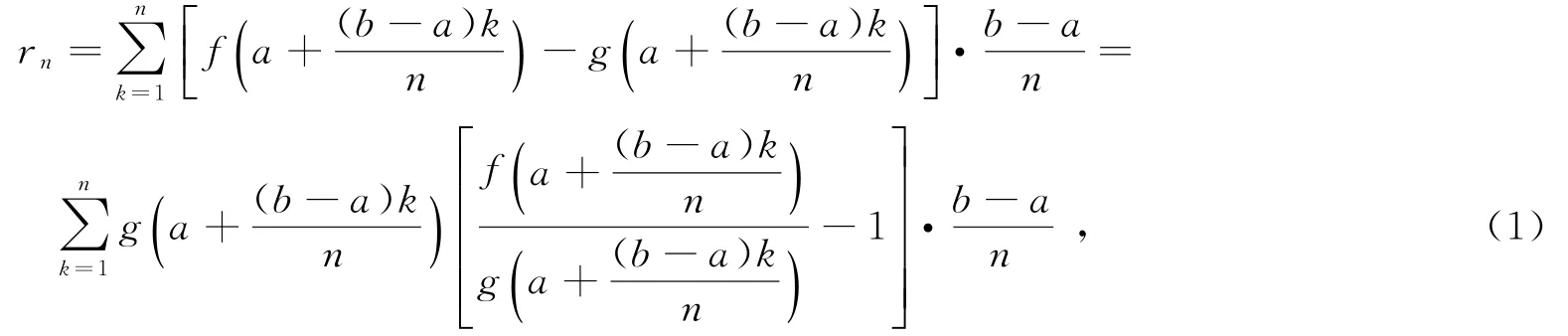
于是

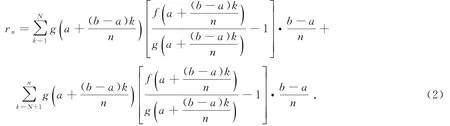
因為f(x),g(x)在[a,b]上可積,所以f(x),g(x)在[a,b]上有界,不妨設|g(x)|≤M,G=,則由式(1)、(2)可得

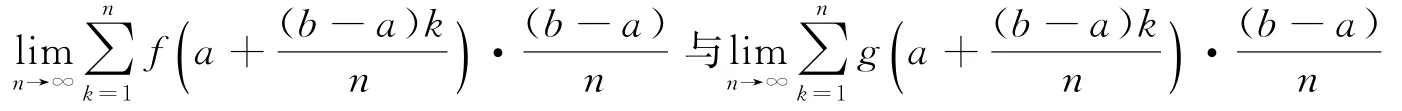
參考文獻:

[1]陳守信.數(shù)學分析選講[M].北京:機械工業(yè)出版社,2009,8:21-24.