一簇金剛石晶格上S 4模型的相變*
尹訓(xùn)昌 劉萬芳 馬業(yè)萬 孔祥木 聞軍 章禮華
1) (安慶師范大學(xué)物理與電氣工程學(xué)院, 安慶 246011)
2) (曲阜師范大學(xué)物理工程學(xué)院, 曲阜 273165)
(2018 年7 月7日收到; 2018 年11 月29日收到修改稿)
采用重整化群和累積展開的方法, 研究了一簇金剛石晶格上 S4 模型的相變, 求得了系統(tǒng)的臨界點. 結(jié)果表明: 當(dāng)分支數(shù) m=2 和 m>12 時, 該系統(tǒng)只存在一個Gauss不動點 K?=b2/2 , u?2=0 ; 當(dāng)分支數(shù)3≤m≤12時, 該系統(tǒng)不僅有Gauss不動點, 還存在一個Wilson-Fisher不動點, 并且后一個不動點對系統(tǒng)的臨界特性產(chǎn)生決定性的影響.
1 引 言
相變是凝聚態(tài)物理學(xué)中的一個重要研究領(lǐng)域,它是自然界中的一種普遍現(xiàn)象, 如人們熟知的水的氣態(tài)和液態(tài)轉(zhuǎn)變就屬于相變. 根據(jù)自旋模型的自旋取值不同, 可分為離散型和連續(xù)型兩種不同的模型. 離散模型只能取一些分離的有限數(shù)值, Ising模型和Potts模型是兩種最有代表性的離散模型. 而連續(xù)模型則允許在整個實數(shù)空間取連續(xù)值, 如S4模型和Gauss模型. 起初人們主要研究具有平移對稱性的平移對稱晶格上自旋模型的相變, 隨著研究的逐漸深入, 人們對具有高度自相似性的分形晶格產(chǎn)生了濃厚的興趣. 20世紀(jì)80年代, Gefen等[1-4]率先研究了幾種簡單有規(guī)分形上離散模型的相變,求得了一系列有意義的結(jié)論. 此后, 分形晶格上的相變問題得到了越來越多的重視, 出現(xiàn)了許多有趣的成果[5-21]. 1999年, 孔祥木等[13]研究了金剛石晶格(2DH)上Gauss模型的相變, 得到了該系統(tǒng)的臨界點. 前人的研究發(fā)現(xiàn): 分形晶格上的Ising模型只有當(dāng)分形維數(shù)大于或等于2時才存在有限溫度的相變; 分形晶格上的Gauss模型存在有限溫度的相變, 臨界點數(shù)值的變化依賴于分形維數(shù); 分形晶格上S4模型總是存在一個Gauss不動點,Wilson-Fisher不動點是否出現(xiàn)主要取決于分形維數(shù)的數(shù)值. 本文主要研究具有m個分支數(shù)目的金剛石晶格 (mDH)上S4模型的相變, 和 Gauss模型相比較,S4模型具有一個很大的優(yōu)點, 即增加了一個表示四次方項的參數(shù), 它更加接近自然界中的真實鐵磁系統(tǒng). 因此, 研究S4模型的相變問題可以更好地解釋自然界中的相變. 采用實數(shù)空間重整化群變換并結(jié)合累積展開的方法, 我們研究了一簇金剛石晶格上S4模型的相變.
2 mDH晶格和S4模型
為了便于理解, 我們以兩個分支的金剛石晶格(2DH)為例闡述mDH的生成過程. 它的構(gòu)造過程見圖1, 先定義由兩個格點和一個鍵組成的圖形作為一個基元(即n=0 級), 再把6個基元依次排列形成一個生成元(即n=1 級), 然后生成元的每一個鍵再用生成元本身替換, 這樣的步驟一直重復(fù)下去, 最后得到的晶格為金剛石晶格. 用同樣的方法, 可以得到mDH晶格. 該晶格屬于非均勻分形, 即格點上的配位數(shù)因格點的位置不同而不同.它的分形維數(shù)和分岔度分別為df=1+lnm/ln3 和R=∞. 本文研究的金剛石晶格本質(zhì)上是由迭代產(chǎn)生的具有自相似性的分形晶格, 只不過從外形上看與金剛石的形狀相類似, 我們形象地把它簡稱為金剛石晶格, 它不同于固體物理中的具有周期性的金剛石晶格.

圖1 金剛石晶格的構(gòu)造過程Fig.1. Constructional procedure of diamond lattice.
mDH晶格上S4模型的約化的有效哈密頓量為

其中參數(shù)K表示格點自旋si和sj之間的約化相互作用,bi表示格點i位置上的Gauss分布常數(shù), 參數(shù)ui代表格點i位置上的四次方項相互作用. 為了求解此種晶格上的相變, 假設(shè)Gauss分布常數(shù)bi和四次方項相互作用ui取決于格點i的配位數(shù)qi, 即滿足等式

3 重整化群變換和累積展開
為了方便描述, 選取mDH晶格的生成元來說明重整化群過程(圖2). 為了避免混淆, 重整化群變換前后的格點位置用不同的字母和數(shù)字來表示,且每個格點上的配位數(shù)與格點的位置相關(guān). 通過分析可知2,···,m). 根據(jù)(1)式, 生成元的有效哈密頓量寫為

其中

圖2 mDH晶格的重整化群過程Fig.2. The renormalization group procedure of mDH lattice.


其中大寫字母P表示一個與格點自旋無關(guān)的重整化群變換常數(shù), 而H′則代表變換后的有效哈密頓量.
為了方便計算, 把有效哈密頓量分解成H0和V兩個表達式, 并把表達式V看作H0的微擾進行計算. 根據(jù)正則系統(tǒng)配分函數(shù)的定義, 容易得到

下面定義部分跡 (PT) 為

重新改寫(8)式為

其中

(10)式稱為累積平均.
因為V是一個十分小的微擾項, 做級數(shù)展開為

把(11)式代入(9)式, 部分跡改寫為

消 約 掉 內(nèi)部 格 點 1,2,···,m和的自旋后, 該系統(tǒng)的有效的哈密頓量重新寫為

根據(jù) (12)式得到

其中

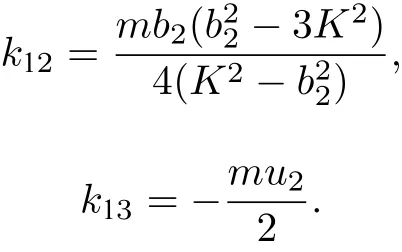
利用(5)式和(10)式, 計算得到
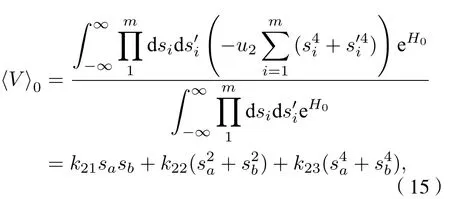
其中

應(yīng)用(5), (10)和(15)式, 可以得到

式中

通過 (13)—(16)式, 經(jīng)過重整化群變換后, 得到系統(tǒng)的有效的哈密頓量為

為了滿足重整化群變換前后系統(tǒng)的有效哈密頓量形勢保持一致的特點, 對自旋變量進行重新標(biāo)度, 定義自旋變量重新標(biāo)度后系統(tǒng)的有效哈密頓量為

其中

(20)式和(21)式為該系統(tǒng)重整化群變換的遞推關(guān)系.
4 計算結(jié)果
根據(jù)上面得到的遞推關(guān)系, 通過計算得到下面的結(jié)果: 1)在mDH晶格的分支數(shù)表m=2 和兩種情況下, 該晶格上的S4模型只存在一個不動點, 即Gauss不動點2)當(dāng)mDH晶格的分支數(shù)滿足 3 ≤m≤12 時, 該晶格上的S4模型不但有Gauss不動點, 而且還發(fā)現(xiàn)一個Wilson-Fisher不動點, 不同的分支數(shù)m所對應(yīng)的Wilson-Fisher不動點的數(shù)值如表1所列. 根據(jù)重整化群的標(biāo)度變換理論, 可以計算出當(dāng)分支數(shù)滿足 3 ≤m≤12 時, Wilson-Fisher不動點附近關(guān)聯(lián)長度的臨界指數(shù)ν的數(shù)值(表1).

表1 mDH晶格上 S4 模型的Wilson-Fisher不動點和關(guān)聯(lián)長度 ν的數(shù)值Table 1. Wilson-Fisher fixed point of S4 model on mDH lattices and the value of correlation length ν.
5 結(jié) 論
應(yīng)用實空間重整化群和累積展開的方法, 研究了mDH晶格上S4模型的相變, 得到了如下結(jié)論:1)當(dāng)分支數(shù)即分形維數(shù)df=1.63和時, 該系統(tǒng)只存在 Gauss不動點其臨界點與該晶格上Gauss模型的臨界點相同, 表明這兩個系統(tǒng)屬于同一個普適類; 2)當(dāng)分支數(shù)符合 3 ≤m≤12 , 即分形維數(shù)2≤df≤3.26時, 該晶格上的S4模型同時存在Gauss不動點和Wilson-Fisher不動點, 并且后一個不動點對系統(tǒng)的臨界特性的影響起主導(dǎo)作用. 進一步研究發(fā)現(xiàn),mDH晶格上S4模型的臨界點的個數(shù)取決于分形維數(shù), 這與平移對稱晶格上的S4模型的相變依賴于空間維數(shù)十分類似.

