基于分數(shù)階累加的灰色GM(1,1|sin)模型及其應(yīng)用

李亞男

(廣東理工學(xué)院基礎(chǔ)教學(xué)部,廣東肇慶526100)

1 引言

針對“小樣本、貧信息”的系統(tǒng)序列的預(yù)測問題,鄧聚龍教授提出了灰色系統(tǒng)理論[1],其中灰色預(yù)測是該理論中的核心體系.GM(1,1)模型作為灰色預(yù)測模型中的典型代表,已被廣泛應(yīng)用于眾多領(lǐng)域[2?4].研究表明,該模型對近似齊次指數(shù)律的數(shù)據(jù)序列的模擬預(yù)測具有較高的精度,而對其他一般序列尤其是振蕩序列的模擬預(yù)測效果并不理想.為拓廣灰色預(yù)測模型的適用范圍,許多學(xué)者針對不同類型的序列進行了深入研究,提出了一系列的灰色預(yù)測模型.針對非齊次指數(shù)律特征的數(shù)據(jù)序列的預(yù)測問題,戰(zhàn)立青等[5]提出了NHGM(1,1,k)模型,并將其應(yīng)用于北京地鐵客流量和江蘇省財政科技投入預(yù)測中;針對部分指數(shù)特征并含時間冪次項的數(shù)據(jù)序列的預(yù)測問題,錢吳永等[6]提出了GM(1,1,tα)模型,并將其應(yīng)用于某省沿海高速公路軟土地基沉降預(yù)測中;為更好地描述系統(tǒng)的非線性的本質(zhì),王正新等[7]提出了GM(1,1)冪模型,并將其應(yīng)用于南京市水路貨運量預(yù)測中;為減少以離散形式估計參數(shù)且用連續(xù)函數(shù)模擬預(yù)測過程中產(chǎn)生的誤差,謝乃明等[8,9]提出了離散灰色預(yù)測模型,并將其應(yīng)用于純指數(shù)序列模擬中;針對振蕩序列的預(yù)測問題,毛樹華等[10]構(gòu)建了GM(1,1|sin)模型,并將其應(yīng)用于城市交通流的模擬預(yù)測中.相比于傳統(tǒng)GM(1,1)模型,以上拓展模型在各自應(yīng)用中都取得了更好的模擬預(yù)測效果,具有一定的實用性.

為充分利用系統(tǒng)的新信息,本文結(jié)合分數(shù)階累加思想[11,12],將文獻[10]的GM(1,1|sin)模型中對原始序列的一階累加方式轉(zhuǎn)變?yōu)榉謹?shù)階累加.由于GM(1,1|sin)模型是利用離散方程估計參數(shù),而預(yù)測時采用的是連續(xù)函數(shù),所以在從離散到連續(xù)的轉(zhuǎn)換過程中不可避免地會產(chǎn)生誤差.為盡量減少轉(zhuǎn)換誤差,本文在分數(shù)階累加的基礎(chǔ)上,對GM(1,1|sin)模型的白化微分方程進行推導(dǎo),構(gòu)建了分數(shù)階累加GM(1,1|sin)模型.由于模型參數(shù)的不同,模擬預(yù)測精度也有所不同,本文采用粒子群算法對模型參數(shù)進行優(yōu)化,使模型具有最高的模擬精度,且更加有效應(yīng)用于振蕩序列的模擬預(yù)測.最后以城市交通流預(yù)測為例,證實了與GM(1,1|sin)模型相比,本文提出的分數(shù)階累加GM(1,1|sin)模型顯著提高了預(yù)測精度.

2 GM(1,1|sin)模型簡介

定義 1 設(shè)非負序列X(0)={x(0)(1),x(0)(2),···,x(0)(n)},稱X(1)={x(1)(1),x(1)(2),···,x(1)(n)}為X(0)的一階累加生成序列,其中

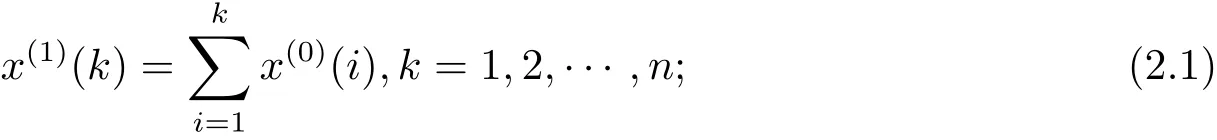
Z(1)={z(1)(1),z(1)(2),···,z(1)(n)}為X(1)的緊鄰均值生成序列,其中

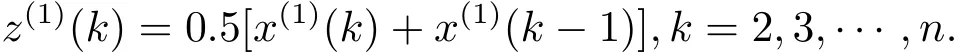
定義2 方程

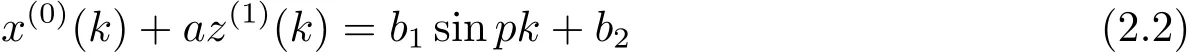
稱為GM(1,1|sin)模型.將一階微分方程

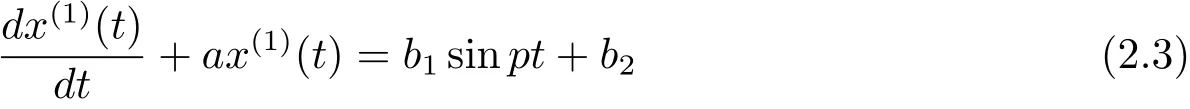
稱為GM(1,1|sin)模型的白化方程.

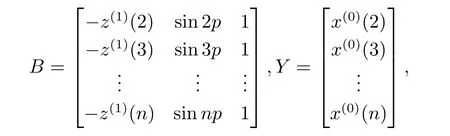
則GM(1,1|sin)模型參數(shù)列的最小二乘估計滿足

在已知p值的前提下,利用方程(2.4)可求解得到模型的各個參數(shù),再將這些參數(shù)代入到白化方程(2.3)中,則可求出微分方程的數(shù)值解即模型的預(yù)測函數(shù).從預(yù)測系統(tǒng)的角度出發(fā),模型的預(yù)測函數(shù)即為模型的時間響應(yīng)函數(shù),對其離散化可得到時間響應(yīng)序列(k=1,2,···).根據(jù)一階累加生成公式(2.1),對做一階累減還原可以得到原始序列的模擬值(k=1,2,···).

一階累減還原值為

3 基于分數(shù)階累加的GM(1,1|sin)模型的構(gòu)建

定義 3 設(shè)非負序列X(0)={x(0)(1),x(0)(2),···,x(0)(n)},稱X(r)={x(r)(1),x(r)(2),···,x(r)(n)}為X(0)的r(r≥0)階累加生成序列,其中

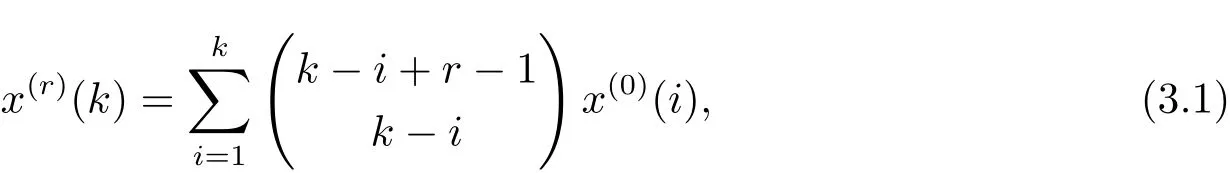
且規(guī)定

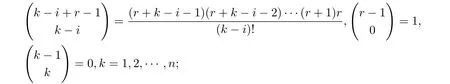
稱矩陣

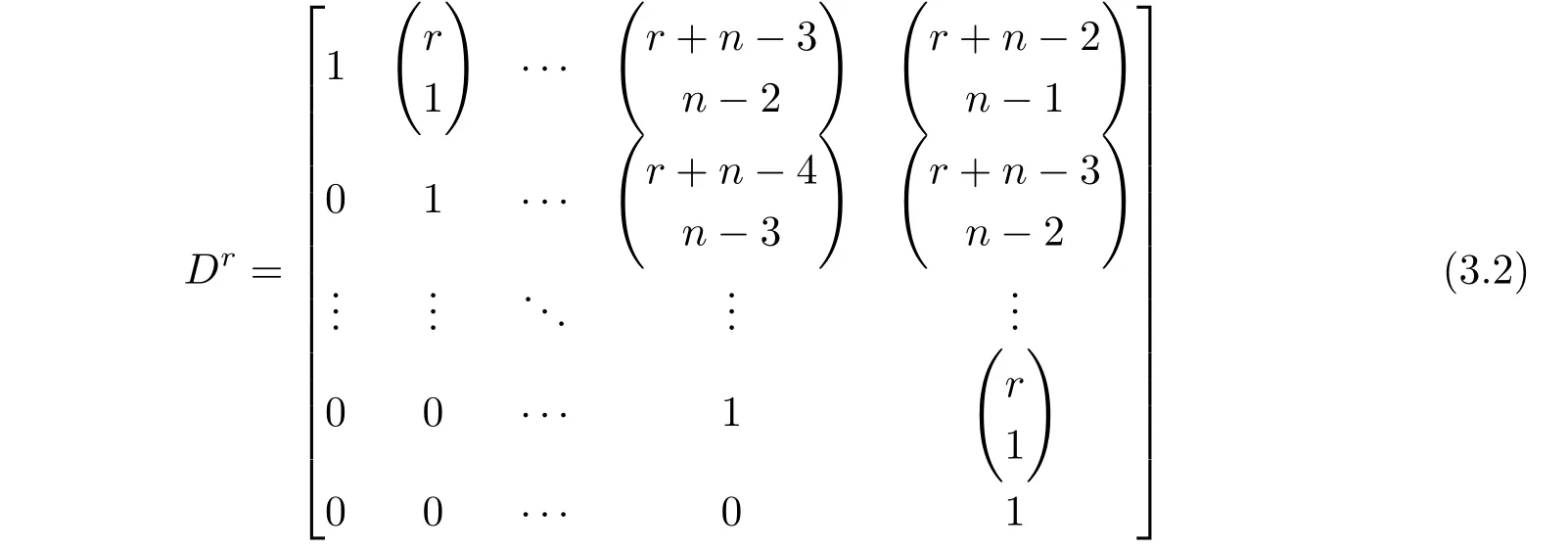
為r階累加生成矩陣,X(r)可表示為

稱Z(r)={z(r)(1),z(r)(2),···,z(r)(n)}為X(r)的緊鄰均值生成序列,其中

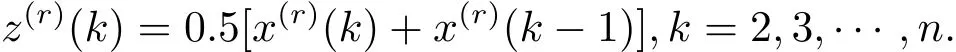
由于GM(1,1|sin)模型利用離散方程(2.2)估計參數(shù),且通過由微分方程(2.3)求解得到的時間響應(yīng)序列進行模擬預(yù)測,所以在從離散到連續(xù)的轉(zhuǎn)換過程中不可避免地產(chǎn)生誤差,此誤差將直接影響到模型的模擬預(yù)測精度.為盡量減少此誤差,以提高模型的模擬預(yù)測精度,本文利用積分運算對白化方程進行推導(dǎo),得到近似程度較高的離散方程.

現(xiàn)對序列X(r)建立結(jié)構(gòu)形式同方程(2.3)的一階線性微分方程

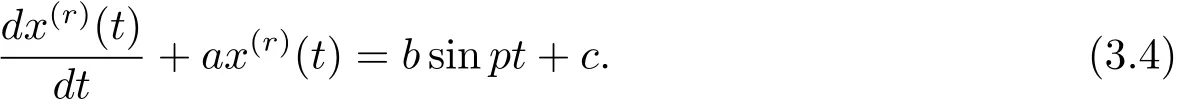
在區(qū)間[k?1,k]上對式(3.4)兩邊同時積分,得

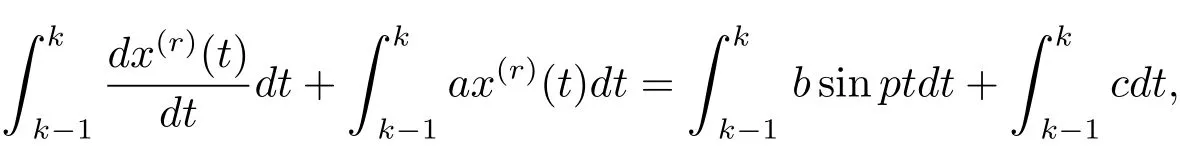
則

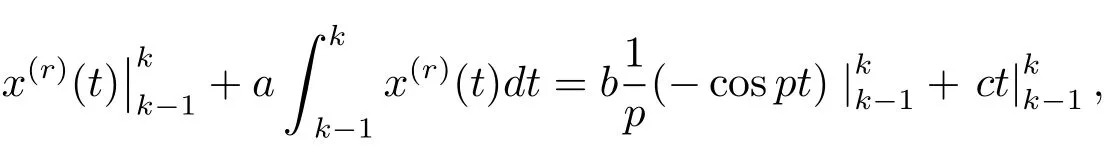
即

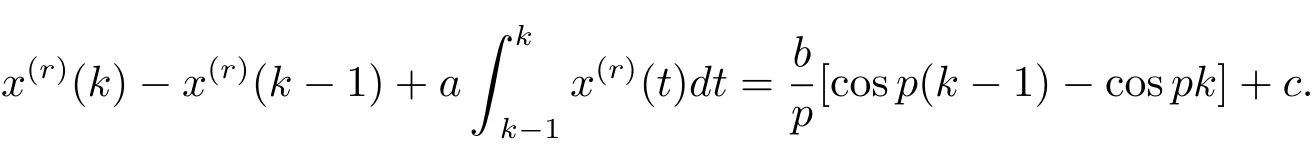
利用三角函數(shù)和差化積公式,可得

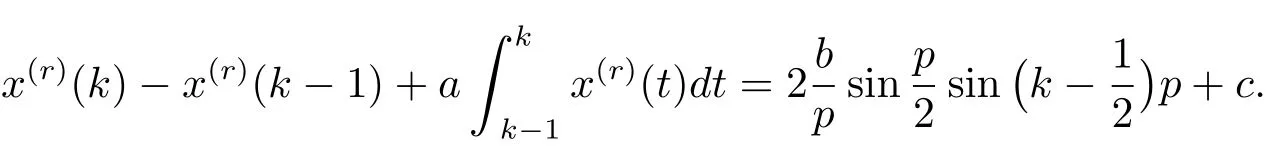
用背景值z(r)(k)近似代替,并作如下定義.

定義4 稱方程

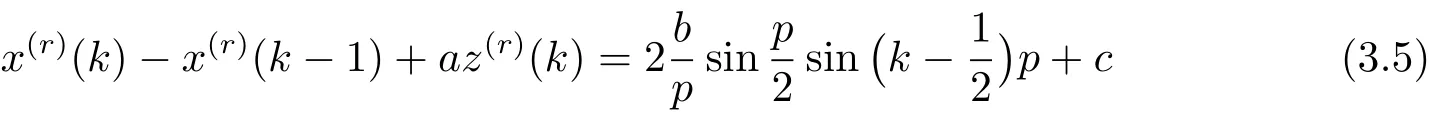
為基于r階累加的GM(1,1|sin)模型(簡稱r階GM(1,1|sin)模型).方程(3.4)為模型的白化方程.

令

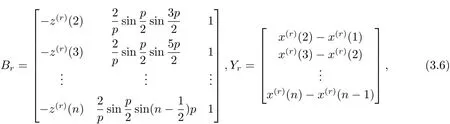
由最小二乘估計可得模型參數(shù)列

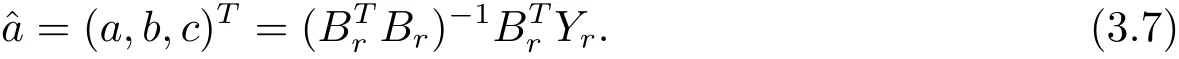
同GM(1,1|sin)模型的預(yù)測原理,將求解得出的參數(shù)代入方程(3.4)可得到模型的時間響應(yīng)函數(shù)(t).對其離散化可得模型的時間響應(yīng)序列(k)(k=1,2,···),再經(jīng)r階累減還原可得原始序列的模擬值(k)(k=1,2,···).

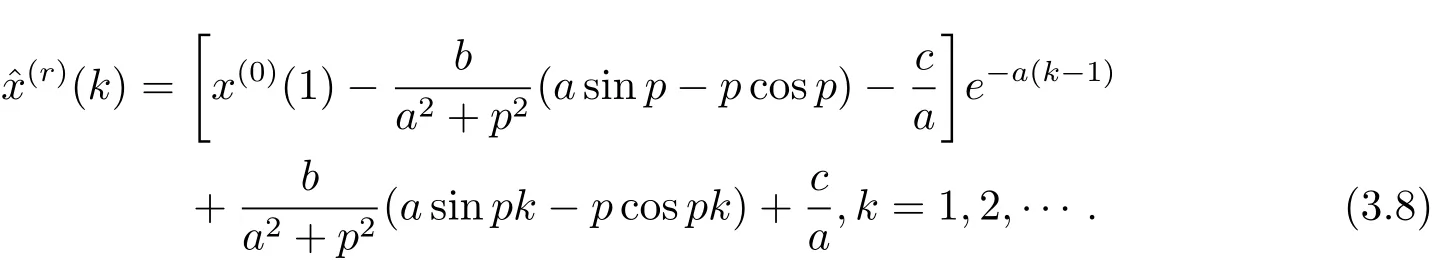
r階累減還原值為

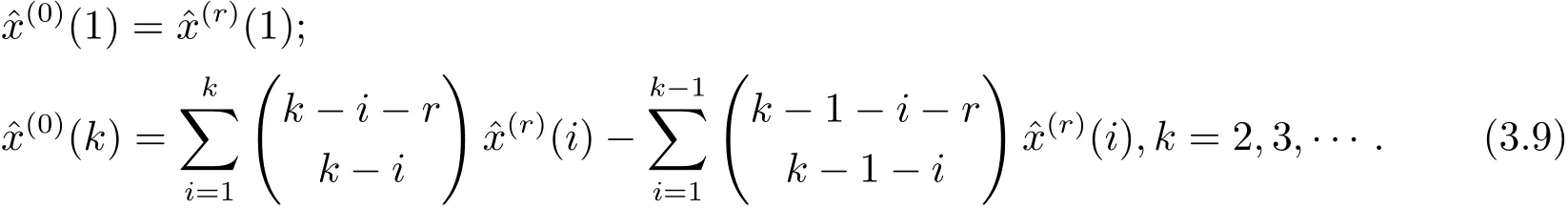
證 由于r階GM(1,1|sin)模型的白化方程(3.4)為非齊次的一階線性微分方程,若令P(t)=a,Q(t)=bsinpt+c,則由非齊次的一階線性微分方程的通解公式可得

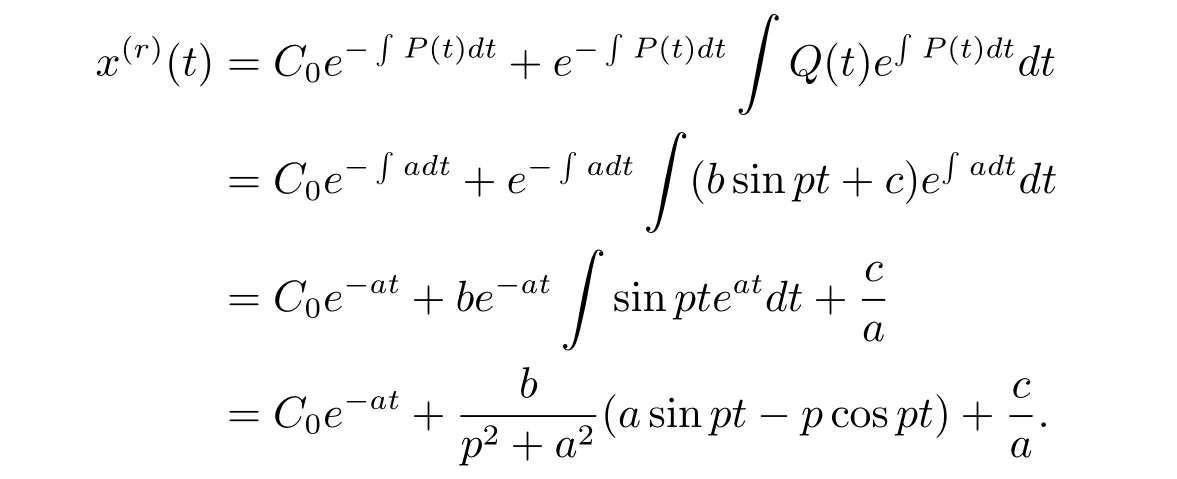
令t=k,則x(r)(t)=x(r)(k).于是可得r階GM(1,1|sin)模型的時間響應(yīng)序列為

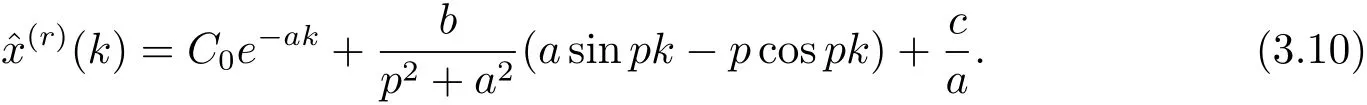
令k=1,得

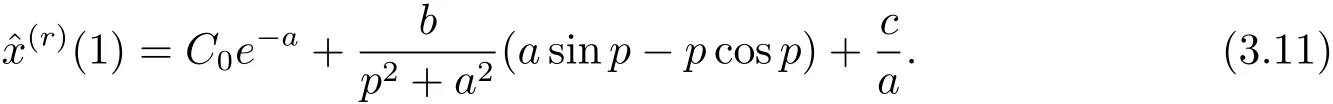
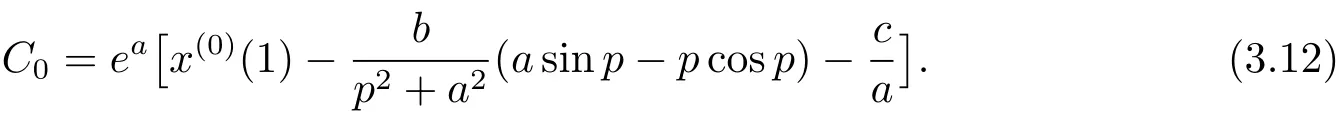
將C0代入式(3.10),得

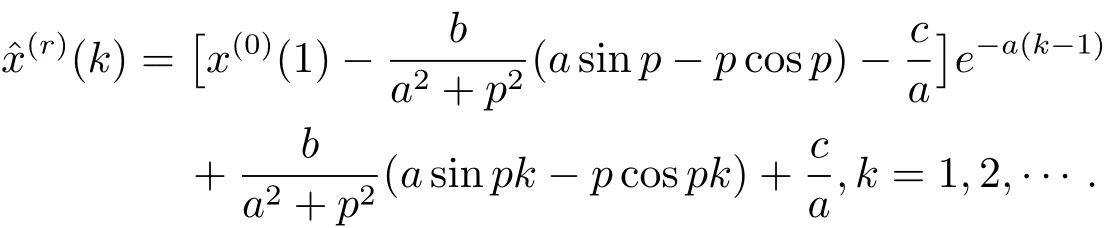
由于X(r)=X(0)Dr(其中Dr為定義3中r階累加生成矩陣),則與原始序列X(0)的模擬值之間滿足.又矩陣Dr的行列式,則矩陣Dr可逆.故.于是r階累減還原值為

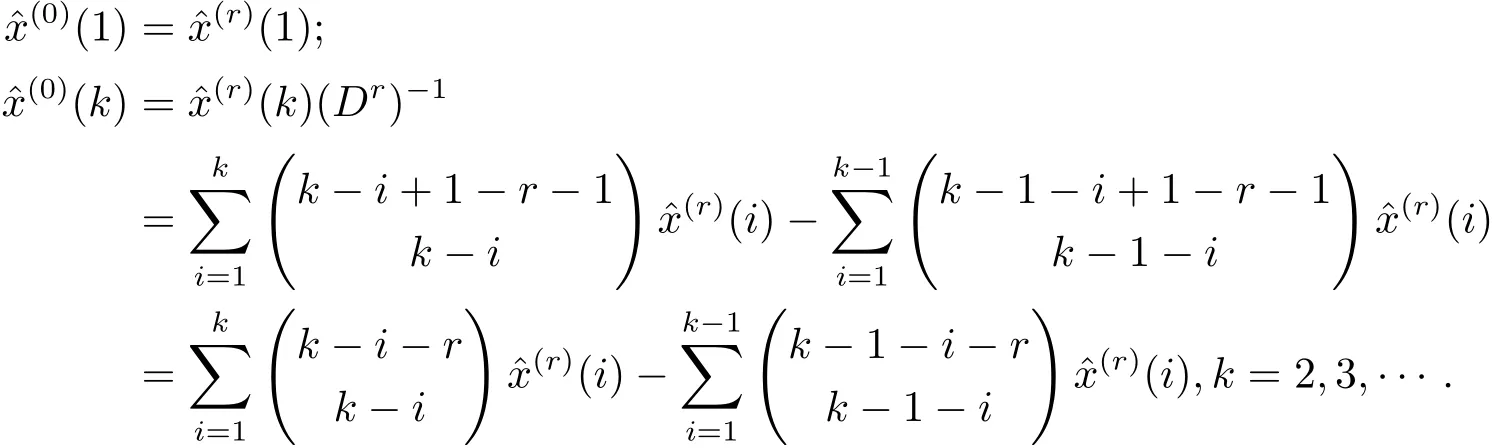
4 r階GM(1,1|sin)模型參數(shù)p和累加階數(shù)r的確定

上述r階GM(1,1|sin)模型是基于參數(shù)p和累加階數(shù)r確定的前提下建立的.一般情況下,p和r的取值不同,模型的模擬精度也會相應(yīng)不同.平均相對誤差是判別灰色預(yù)測模型的模擬效果優(yōu)劣的常用準則,因此,為達到最優(yōu)的模擬效果,本文以平均相對誤差最小化為目標,模型參數(shù)之間的關(guān)系以及p和r自身的取值范圍為約束,建立如下非線性優(yōu)化模型

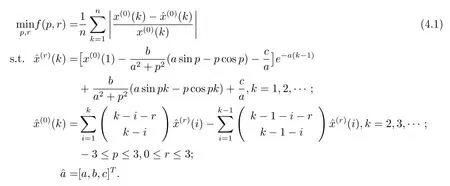
為得出p和r的最優(yōu)值,本文采用粒子群優(yōu)化算法(簡記為PSO)對該優(yōu)化模型進行求解.PSO是由Eberhart博士和Kennedy博士于1995年提出的一種新的進化算法[13],其源于對鳥群捕食的行為研究.由于PSO具有概念簡單、參數(shù)少和易于計算與編程等優(yōu)點,所以在函數(shù)優(yōu)化和神經(jīng)網(wǎng)絡(luò)訓(xùn)練等領(lǐng)域得到了廣泛的應(yīng)用[14].

PSO的基本思路是:首先對優(yōu)化問題初始化一組隨機解,每個隨機解都視為搜索空間中的“粒子”,然后通過迭代找到最優(yōu)解.在每一次迭代中,所有粒子都有一個由被優(yōu)化的函數(shù)決定的適應(yīng)值.基于適應(yīng)值,粒子本身所找到的最優(yōu)解稱為個體極值(pBest),整個種群目前找到的最優(yōu)解稱為全局極值(gBest).當找到這兩個極值時,粒子根據(jù)以下公式來更新自己的速度v和位置x:

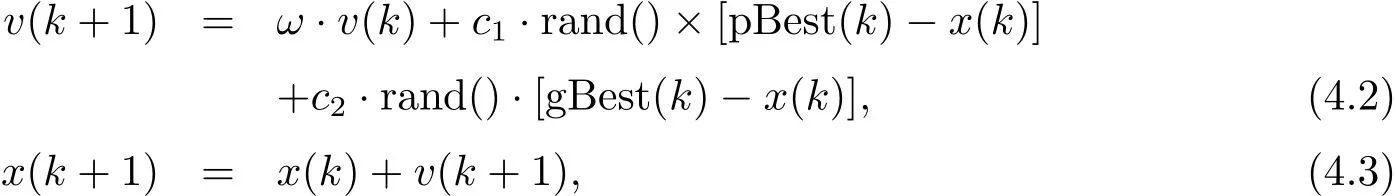
其中ω是慣性權(quán)重,它決定了粒子先前速度對當前速度的影響程度,起到平衡算法全局搜索和局部搜索能力的作用[15].當取值范圍在0.9和1.2之間時,優(yōu)化效果較好;c1和c2是學(xué)習(xí)因子,這兩個常數(shù)使粒子具有自我總結(jié)和向群體中優(yōu)秀個體學(xué)習(xí)的能力,從而向最優(yōu)點靠近.c1和c2通常都取等于2,并且范圍在0和4之間;rand()為在[0,1]之間的隨機數(shù).粒子當前的速度決定了粒子下一步搜索的距離和方向,且有一個最大速度Vmax,最大速度決定粒子在每一次迭代中最大的移動距離,通常設(shè)定為粒子的范圍寬度.整個算法停止準則是達到最大迭代次數(shù)或獲得可以接受的滿意解.

基于粒子群算法的r階GM(1,1|sin)模型的建模求解步驟如下:

步驟1取粒子數(shù)為30,在問題可行域中初始化所有粒子的位置和速度.

步驟2取平均相對誤差即目標函數(shù)(4.1)作為適應(yīng)度函數(shù),計算出每個粒子的適應(yīng)值.分別比較每個粒子的適應(yīng)值與個體極值pBest和全局極值gBest之間的關(guān)系,如果前者優(yōu)于后者,則將當前粒子位置設(shè)置為pBest位置和gBest位置.

步驟3按照式(4.2)和(4.3)更新粒子的速度和位置.

步驟4循環(huán)回到步驟2.終止條件設(shè)置為達到最大迭代次數(shù)2000或所有個體極值的最大值與全局極值之間的誤差小于10?25.若滿足終止條件,則轉(zhuǎn)到步驟5.

步驟5輸出全局極值以及相應(yīng)的原始序列的模擬值?x(0)(k),算法結(jié)束.

5 應(yīng)用實例

為了驗證本文提出的分數(shù)階累加GM(1,1|sin)模型的模擬預(yù)測效果,以文獻[10]中的數(shù)據(jù)為例,原始數(shù)據(jù)為紐約市某天6時至18時的交通流量(以1小時為間隔),即

易見,該序列為振蕩序列.為體現(xiàn)本文提出的新模型的優(yōu)化效果,對序列X(0)分別建立文獻[10]中GM(1,1|sin)模型x(0)(k)+az(1)(k)=b1sinpk+b2,累加階數(shù)r=1時的r階GM(1,1|sin)模型和r階GM(1,1|sin)模型得到的模擬值及平均相對誤差結(jié)果見表1和圖1.

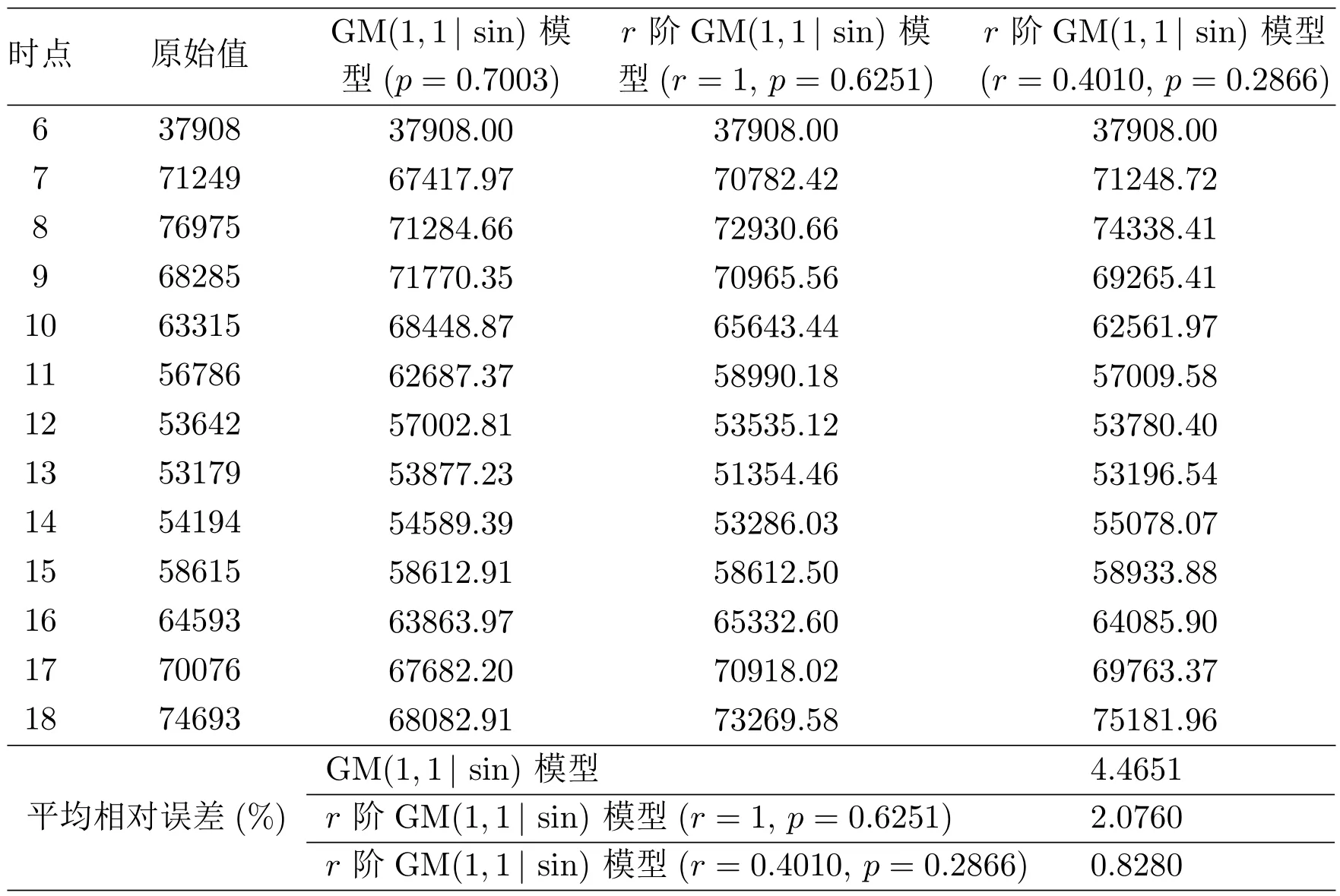
表1:三種模型的模擬結(jié)果比較

圖1:三種模型對交通流的模擬預(yù)測曲線

由表1可以看出,累加階數(shù)為1時的r階GM(1,1|sin)模型的平均相對誤差為2.0760%,顯著小于GM(1,1|sin)模型的4.4651%,說明新模型能有效較少離散到連續(xù)的轉(zhuǎn)換誤差.同時,r階GM(1,1|sin)模型的平均相對誤差僅為0.8280%,進一步提高了模擬精度.從圖1同樣可看出,r階GM(1,1|sin)模型的預(yù)測效果要顯著優(yōu)于GM(1,1|sin)模型.綜合分析說明,與GM(1,1|sin)模型相比,本文提出的r階GM(1,1|sin)模型能更準確地反映交通流的變化規(guī)律,能更好地適應(yīng)振蕩序列的模擬預(yù)測.

6 結(jié)語

由于振蕩序列具有隨機性和不穩(wěn)定性的特點,所以利用傳統(tǒng)灰色模型難以得到滿意的預(yù)測效果.為此,本文提出了基于分數(shù)階累加的GM(1,1|sin)模型,一方面利用了分數(shù)階蘊含著的“in between”思想,能充分利用系統(tǒng)的新信息;另一方面利用了對白化方程推導(dǎo)的方式構(gòu)建模型,能有效減少模型從離散到連續(xù)的轉(zhuǎn)換中所帶來的誤差.實例表明,采用粒子群算法找到最優(yōu)參數(shù),可使新模型對振蕩序列的預(yù)測效果好于現(xiàn)有的GM(1,1|sin)模型,并且達到較高的精度.