SHARP BOUNDS FOR TOADER-TYPE MEANS IN TERMS OF TWO-PARAMETER MEANS?
(楊月英)
School of Mechanical and Electrical Engineering,Huzhou Vocational&Technical College,Huzhou 313000,China
E-mail:yyy1008@163.com
Weimao QIAN(錢偉茂)
School of Continuing Education,Huzhou Vocational&Technical College,Huzhou 313000,China
E-mail:qwm661977@126.com
Hongwei ZHANG(張宏偉)
School of Mathematics and Statistics,Changsha University of Science&Technology,Changsha 410014,China
E-mail:hwzhang2018@163.com
Yuming CHU(褚玉明)?
Department of Mathematics,Huzhou University,Huzhou 313000,China
E-mail:chuyuming2005@126.com;chuyuming@zjhu.edu.cn
Abstract In the article,we prove that the double inequalities hold for all a,b>0 with ab if and only if λ1 and
Key words Geometric mean;arithmetic mean;Toader mean;ontraharmonic mean;complete elliptic integral
1 Introduction
Let a,b>0 and r∈(0,1).Then the geometric mean G(a,b),arithmetic mean A(a,b),quadratic mean Q(a,b),contraharmonic mean C(a,b),Toader mean T(a,b)[1,2],complete elliptic integrals K(r)and E(r)[3–18]of the first and second kinds are given by
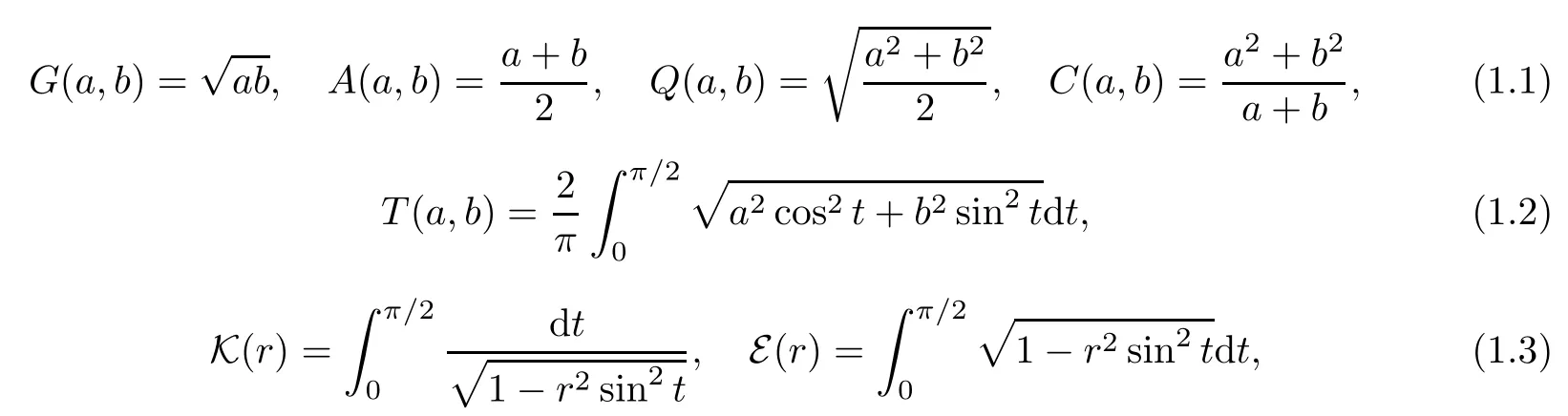
respectively.
From(1.2)and(1.3)we clearly see that
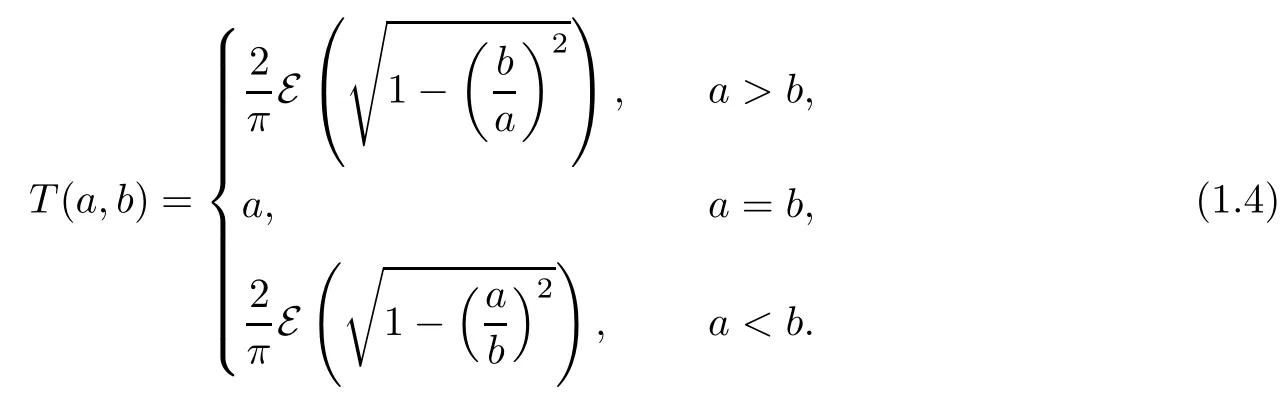
It is well known that K(r)is strictly increasing from(0,1)onto(π/2,∞),that E(r)is strictly decreasing from(0,1)onto(1,π/2),and that they satisfy the following formulae[19]:

Recently,the bounds for the Toader mean have attracted the attention of many researchers.Vuorinen,in[22],conjectured that
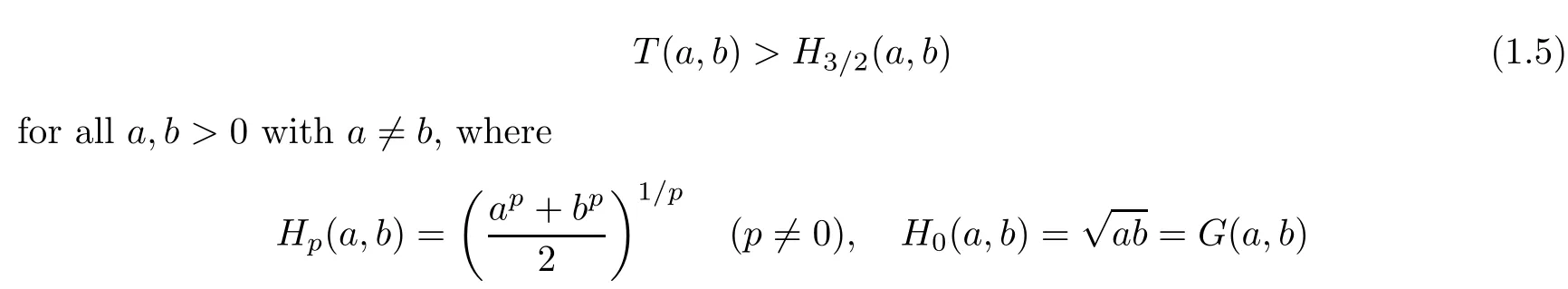
is the p-th H?lder mean.Inequality(1.5)was proved by Barnard,Pearce and Richards in[23],and they proved that H2(a,b)is an upper H?lder mean bound for T(a,b).
In[24],Alzer and Qiu proved that p0=log2/(logπ?log2)=1.5349...is the best possible constant such that the inequality T(a,b)<(a,b)holds for all a,b>0 with a/=b,and proposed that
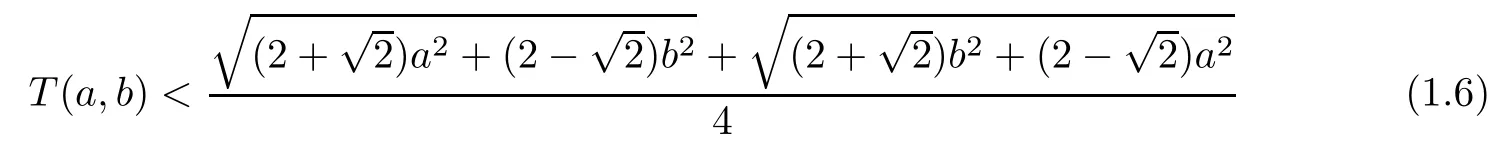
for all a,b>0 with a/=b.
Inequality(1.6)was proved by Kazi and Neuman[25]by using the two-point Gauss-Chebyshev quadrature formula with the remainder given in[26].
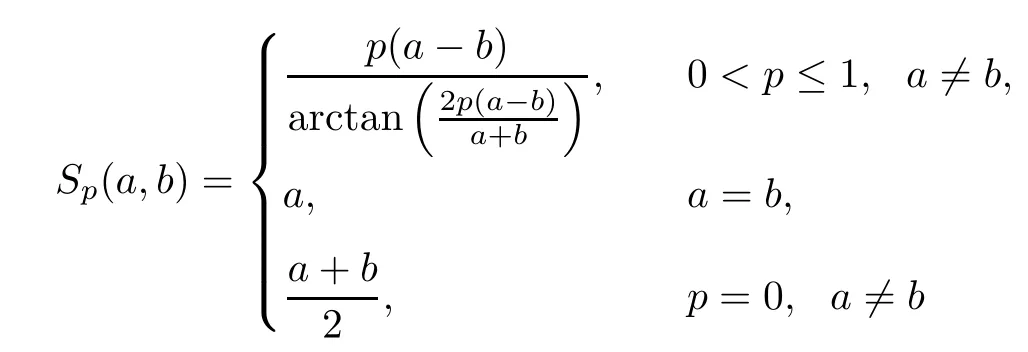
is the generalized Seiffert mean.
In[28,29],the authors proved that the double inequalities
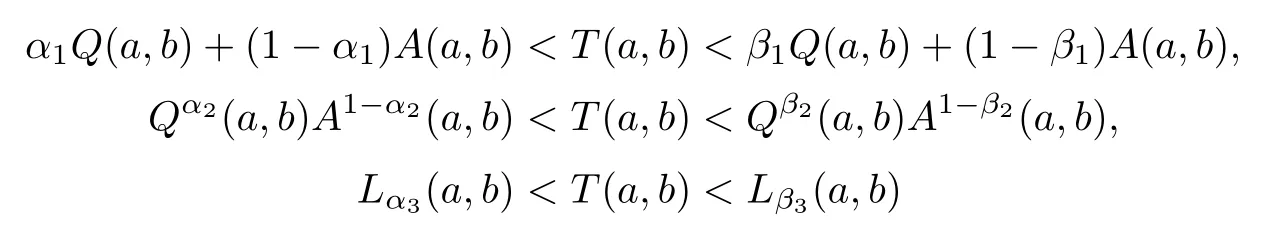
hold for all a,b>0 with a/=b if and only if α1≤1/2,β1≥(4?π)/[(√2?1)π]=0.659...,α2≤1/2,β2≥4?2logπ/log2=0.697...,α3≤0 and β3≥1/4,where Lp(a,b)=(ap+1+bp+1)/(ap+bp)is the p-th Lehmer mean.
Wang et al.[30]established the double inequality

hold for all a,b>0 with a/=b and p∈[1/2,2].The special cases p=1 and p=1/2 of inequality(1.8)were also proved in[32]and[33],respectively.
In[34],Chu et al.proved that the double inequalities

Let p≥1,s≥1/2,λ∈(0,1/2)andμ∈(1/2,1).Then the two-parameter geometricarithmetic mean GAλ,p(a,b)and two-parameter contraharmonic-arithmetic mean CAμ,s(a,b)are defined by
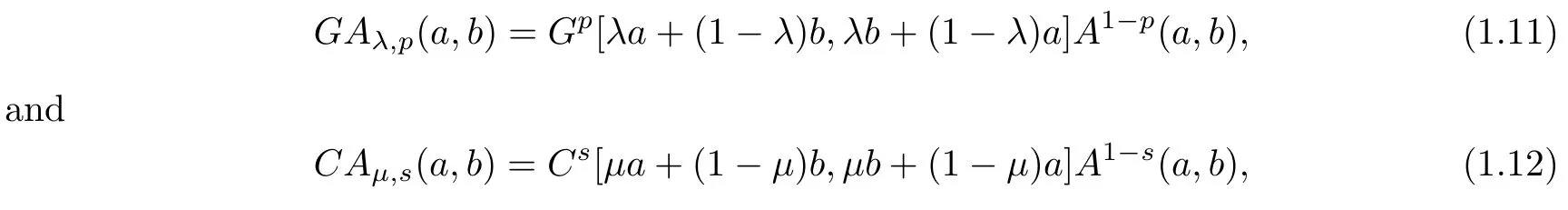
respectively.
From(1.1),(1.7),(1.11)and(1.12),we clearly see that
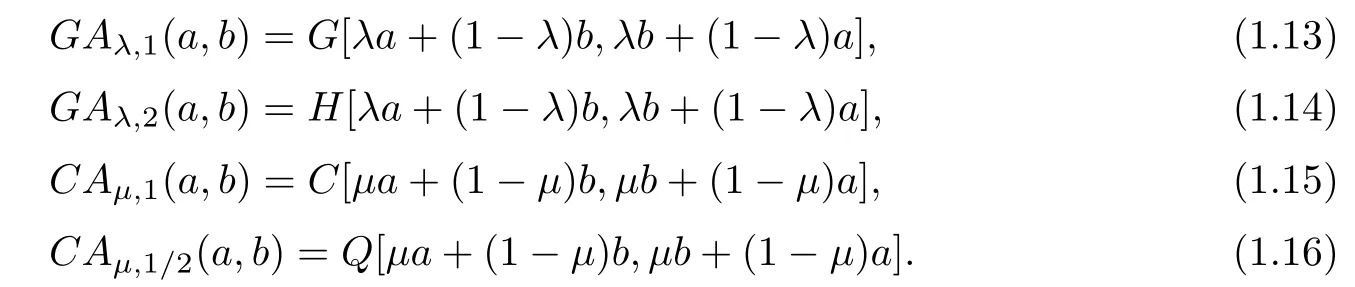
The aim of the article is to find the best possible parameters λ1=λ1(p),μ1=μ1(p)∈(0,1/2)and λ2=λ2(s),μ2=μ2(s)∈(1/2,1)such that the double inequalities
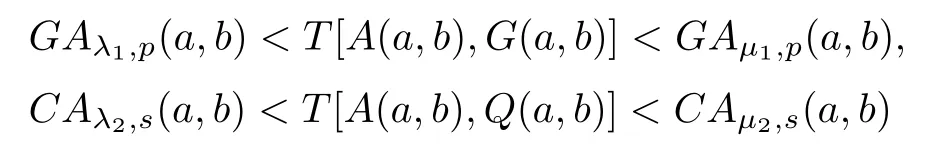
hold for all p≥1,s≥1/2 and a,b>0 with a/=b.
2 Lemmas
In order to prove our main results,we need four lemmas,which we present in this section.
Lemma 2.1The following statements are true:
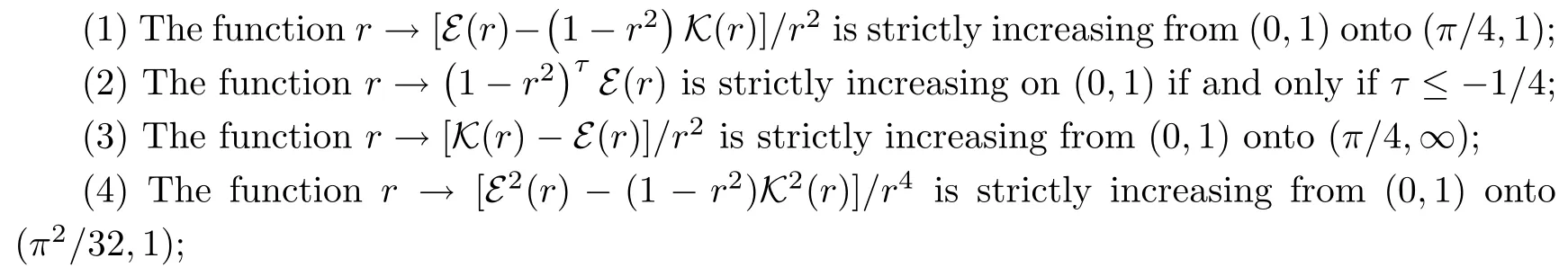
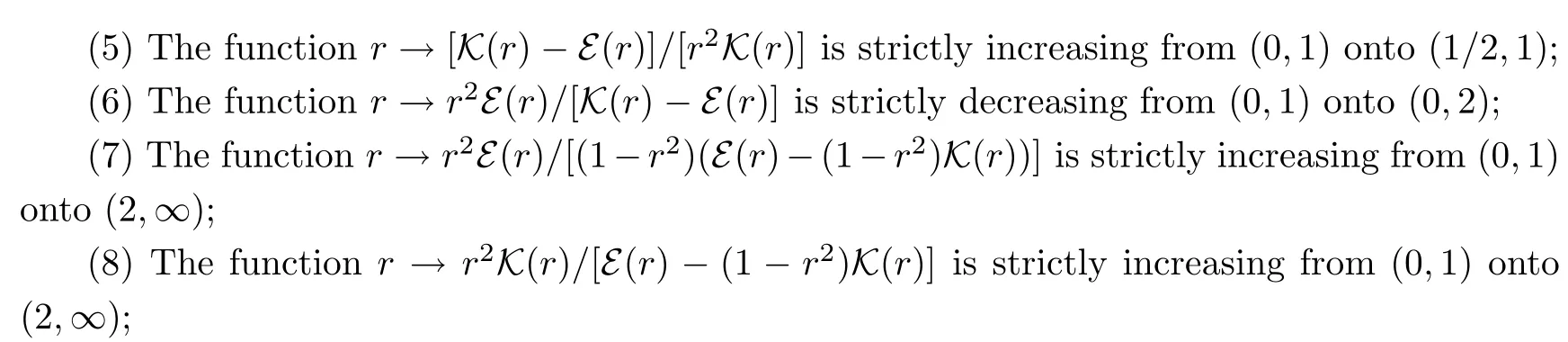
ProofParts(1)–(5)can be found in[19,Theorem 3.21(1)and(8),and Exercises 3.43(11),(16)and(32)].
Part(6)follows easily from part(3)and the monotonicity of E(r)on the interval(0,1),together with the facts that

Lemma 2.3Let u∈[0,1],r∈(0,1),p≥1 and
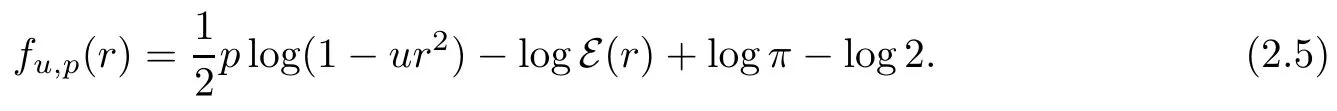
Then one has that
(1)fu,p(r)>0 for all r∈(0,1)if and only if u≤1/(2p);
(2)fu,p(r)<0 for all r∈(0,1)if and only if u≥1?(2/π)2/p.
ProofIt follows from(2.5)that
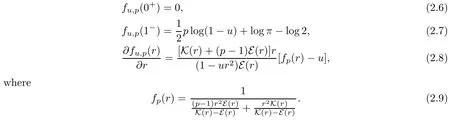
From Lemma 2.1(5)and(6),together with(2.9),we know that the function r→fp(r)is strictly increasing on(0,1)and that
It follows from Lemma 2.2 that the interval[0,1]can be expressed by

We divide the proof into three cases.
Case 1:u≤1/(2p).Then,from(2.8)and(2.10),together with the monotonicity of the function r→fp(r)on the interval(0,1),we get that the function r→fu,p(r)is strictly increasing on(0,1).Therefore,fu,p(r)>0 for all r∈(0,1)follows from(2.6)and the monotonicity of the function r→fu,p(r)on the interval(0,1).
Case 2:u=1.Then equations(2.8)and(2.10),together with the monotonicity of the function r→fp(r)on the interval(0,1),lead to the conclusion that the function r→fu,p(r)is strictly decreasing on(0,1).Therefore,fu,p(r)<0 for all r∈(0,1)follows from(2.6)and the monotonicity of the function r→fu,p(r)on the interval(0,1).
Case 3:1/(2p) We divide the proof into two subcases. Subcase 3.1:1?(2/π)2/p≤u<1.Then(2.7)leads to Therefore,fu,p(r)<0 for all r∈(0,1)follows from(2.6)and(2.11),together with the piecewise monotonicity of the function r→fu,p(r)on the interval(0,1). Subcase 3.2:1/(2p) Therefore,there exists u?∈(u0,1)such that fu,p(r)<0 for u∈(0,u?)and fu,p(r)>0 for u∈(u?,1)follows from(2.6)and(2.12),together with the piecewise monotonicity of the function r→fu,p(r)on the interval(0,1). □ We divide the proof into three cases. Theorem 3.1Let λ1,μ1∈(0,1/2)and p≥1.Then the double inequality Therefore,Theorem 3.3 follows from Lemma 2.4 and(3.2). □ Remark 3.4Let s=1/2,1.Then,from(1.14)and(1.15),we clearly see that inequalities(1.9)and(1.10)can be derived from Theorem 3.3. The following Corollary 3.5 also can be derived directly from(1.1),(1.4),(1.11)and(1.12),as well as Theorems 3.1 and 3.3: Corollary 3.5Let λ1,μ1∈(0,1/2),λ2,μ2∈(1/2,1),p≥1 and s≥1/2.Then the double inequalities



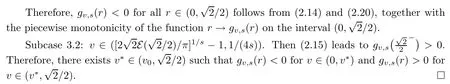
3 Main Results


 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
