具有環(huán)境傳播和生理年齡結(jié)構(gòu)的霍亂模型研究
亢躍男, 郭文丹, 聶麟飛
(新疆大學 數(shù)學與系統(tǒng)科學學院, 新疆 烏魯木齊 830046)
霍亂是一種通過攝入由霍亂弧菌污染的水或食物引起的急性腸道傳染病.霍亂弧菌可以在環(huán)境中存活1~3周, 甚至更長時間, 它主要通過人與人直接傳播或環(huán)境與人間接傳播.自1817年以來霍亂發(fā)生了七次世界性大流行, 據(jù)世衛(wèi)組織估計, 每年大約有130萬至400萬例病例, 以及2.1萬至14.3萬例死亡[1].時至今日, 霍亂仍是威脅全球人類生命健康的重大公共衛(wèi)生問題.
在過去幾十年中, 國內(nèi)外學者建立了許多具有人與人之間或環(huán)境與人之間傳播的霍亂常微分方程模型[2-5],研究了其無病平衡態(tài)和地方病平衡態(tài)的存在性與穩(wěn)定性.眾所周知,在生物種群中異質(zhì)性是廣泛存在的,不同年齡段的人接觸疾病的概率是不同的,從而感染疾病的風險也不同,因此,研究具有年齡結(jié)構(gòu)的傳染病模型是很有必要的.為此,一些國內(nèi)外研究者建立了具有年齡結(jié)構(gòu)的傳染病數(shù)學模型[6-10],討論了年齡在傳染病傳播中的影響.例如,Lin等[8]提出的類年齡結(jié)構(gòu)霍亂模型中考慮了感染者的感染年齡和環(huán)境中病原體的倉室年齡,討論了無病平衡態(tài)和地方病平衡態(tài)的局部穩(wěn)定性和全局穩(wěn)定性.Yang等[9]建立了偏微分方程和常微分方程耦合的人群具有生理年齡的霍亂環(huán)境傳播模型,給出了疾病的基本再生數(shù),討論了年齡對霍亂傳播的影響.基于上述討論,本文將建立人群和環(huán)境病毒均有生理年齡的霍亂傳播偏微分方程模型,討論各類平衡態(tài)的存在性和穩(wěn)定性.
1 模型的建立與正解的存在唯一性
將某地區(qū)的人群分為三類: 易感者類,感染者類和恢復者類,其在t時刻a年齡的密度分別為S(t,a),I(t,a),R(t,a),記環(huán)境中t時刻年齡為a的霍亂弧菌濃度為P(t,a).總?cè)丝诘哪挲g密度函數(shù)為N(t,a)=S(t,a)+I(t,a)+R(t,a).根據(jù)病原體在人群和環(huán)境之間的傳播規(guī)律,易感者以λ1(t,a)的速率接觸染病者而被感染,以λ2(t,a)的速率接觸環(huán)境中的病毒而被感染,這里定義如下感染力函數(shù)[11]:
其中:k(a)表示接觸率;β1(a)表示感染者的傳染率;β2(a)表示環(huán)境中病原體的傳染率.進一步,令b(a)和μ(a)分別表示單位時間內(nèi)年齡為a的人均出生率和死亡率,γ(a)和θ(a)分別表示人類年齡依賴的治療率和自然恢復率,ξ(a)表示感染者的病毒脫落率,δ(a)表示環(huán)境中病原體的自然死亡率.
基于上述假設(shè),建立具有環(huán)境傳播和年齡結(jié)構(gòu)的霍亂模型
(1)
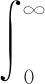
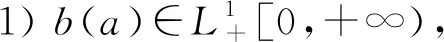
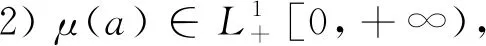
把模型(1)中的前三個方程相加,得
(2)
模型(2)是標準的Mckendrik-Von Forester方程,沿特征線t-a=c(常數(shù))[12]解得
為保證關(guān)于年齡穩(wěn)態(tài)的存在性,假設(shè)人口的凈再生率等于1,即人口總數(shù)處于平衡狀態(tài),則
從而,模型(2)的穩(wěn)態(tài)解為
初始人口分布滿足:S0(a)≥0,I0(a)≥0,R0(a)≥0,S0(a)+I0(a)+R0(a)=N∞(a),則
對模型(1)進行歸一化處理,令
則
從而,模型(1)可改寫為
(3)
式中:s(t,0)=1,i(t,0)=r(t,0)=p(t,0)=0,t>0.s(0,a)=s0(a),i(0,a)=i0(a),r(0,a)=r0(a),p(0,a)=p0(a),且s(t,a)+i(t,a)+r(t,a)=1.
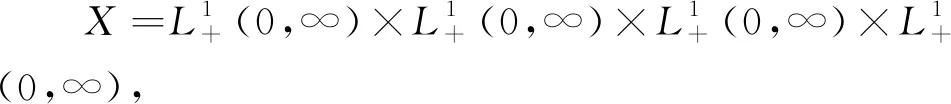

則模型(3)可化為抽象柯西問題
(4)
式中:u(t)=(s(t,·),i(t,·),r(t,·),p(t,·))T,u0(a)=(s0(a),i0(a),r0(a),p0(a))T.顯然,當t>a時,算子A是C0-半群T(t)的無窮小生成元,并且算子B在空間X上連續(xù)Frechet可微.定義兩個集合F={(s,i,r,p)∈X:s≥0,i≥0,r≥0,p≥0}和F0={(s,i,r,p)∈X:0≤s≤1,0≤i≤1,0≤r≤1,0≤p≤K},其中K是正常數(shù).與文獻[13]中引理3.1的證明類似,關(guān)于模型(4)有以下的結(jié)論.
引理1F0是關(guān)于u的正不變集,并且對于X上的初值u0∈F∩D(A),模型(4)存在唯一的經(jīng)典解.
2 無病平衡態(tài)的穩(wěn)定性
利用特征方程推導基本再生數(shù)R0的精確表達式,并證明無病平衡態(tài)的局部和全局漸近穩(wěn)定性.顯然,模型(3)存在無病平衡態(tài)E0=(1,0,0,0).令
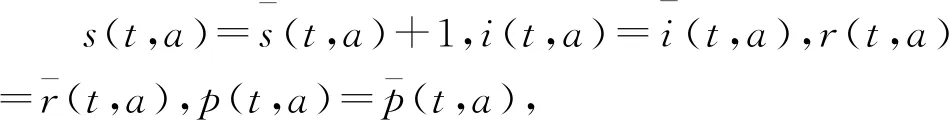
(5)
式中
(6)
式中
(7)
利用常數(shù)變易法求解模型(6)得
(8)
(9)
上式左右兩邊同時除以V0(V0≠0),得到特征方程
(10)
定義基本再生數(shù)[14]R0:=G(0),即
現(xiàn)討論無病平衡態(tài)E0的穩(wěn)定性.
定理1若R0<1,則模型(3)的無病平衡態(tài)E0是局部漸近穩(wěn)定的; 若R0>1,則不穩(wěn)定.
證明由式(10)可知,
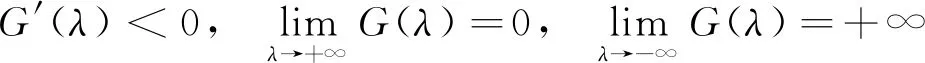
則特征方程(10)存在唯一實根.如果R0<1,即G(0)<1,那么G(λ)=1存在唯一的負實根λ*.進一步考慮方程(10)的復根.設(shè)λ=x+iy是G(λ)=1的任意復根,則
G(λ*)=1=|G(x+iy)|≤G(x)
由于G(λ)是關(guān)于λ單調(diào)遞減的函數(shù),所以Re(λ)=x≤λ*,即方程(10)的所有復根都具有負實部.因此,當R0<1時,模型(3)的無病平衡態(tài)E0是局部漸近穩(wěn)定的.另一方面,如果R0>1,即G(0)>1,那么方程(10)存在唯一的正實根,從而無病平衡態(tài)E0是不穩(wěn)定的.
定理2若R0<1,則模型(3)的無病平衡態(tài)E0是全局漸近穩(wěn)定的.
證明令f(t,a)=(λ1(t,a)+λ2(t,a))s(t,a),由于s(t,a)≤1,故
f(t,a)≤λ1(t,a)+λ2(t,a)=k(a)V(t)
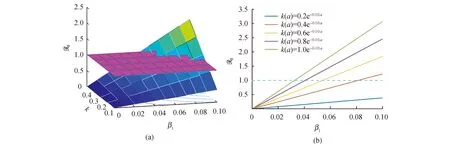
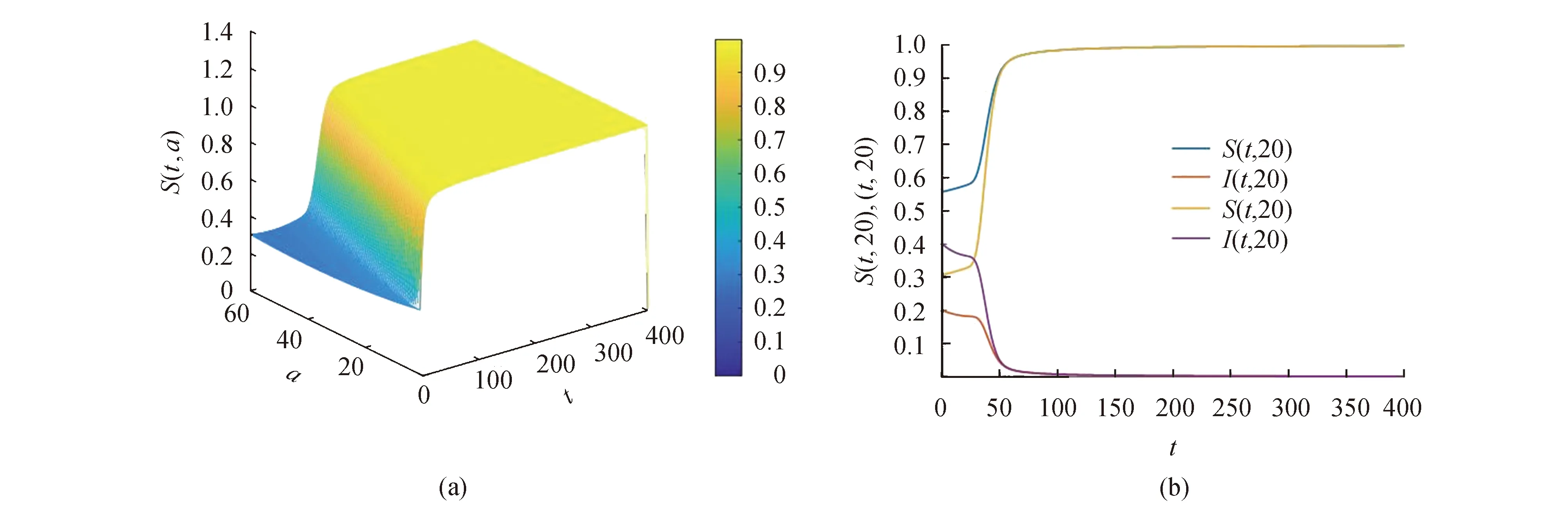
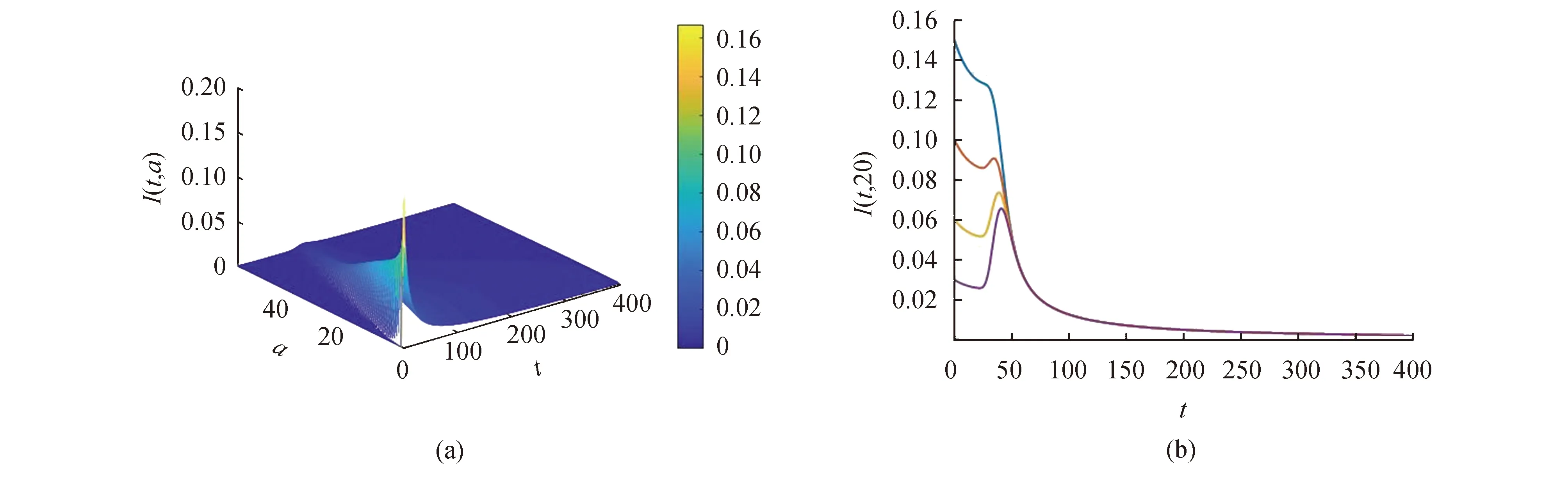
沿著特征線對模型(3)積分(當a (11) 將式(11)中的i(t,a)代入p(t,a)得 (12) 由式(11)中的i(t,a)和式(12)可得 (13) 記常數(shù)M為 則F(a)≤k(a)M.因此, 關(guān)于模型(3)地方病平衡態(tài)的存在性與穩(wěn)定性,有下面的結(jié)論. 定理3當R0>1時,模型(3)存在唯一的地方病平衡態(tài)E*(s*(a),i*(a),r*(a),p*(a)). 證明模型(3)的平衡態(tài)必須滿足如下與時間無關(guān)的常微分方程組: (14) 式中 (15) 根據(jù)模型(14)可得 (16) 將式(16)中的s*(a)代入i*(a)得 (17) 將式(17)代入式(16)中的p*(a)得 (18) 將式(17)和式(18)代入式(15),并將得到的方程左右兩端同時除以V*(V*≠0),則 (19) 令V*=0,則 由于s*(a)+i*(a)+r*(a)=1,且s*(a)>0,所以i*(a)<1.又因為p*(a) H(β(1+K)N)<1 由于H(V*)是關(guān)于V*單調(diào)遞減的函數(shù),并且當R0>1時,有H(0)>1.因此,方程(19)在(0,β(1+K)N)上存在唯一實根.即,當R0>1時,模型(3)存在唯一的地方病平衡態(tài). 討論地方病平衡態(tài)的穩(wěn)定性,將模型(3)在地方病平衡態(tài)E*處線性化,并考慮指數(shù)形式的解 則 (20) 式中 (21) (22) 利用常數(shù)變易法求解模型(21)得 (23) 把式(23)中的y(a)代入u(a)得 (24) 根據(jù)J(ω)的表達式,把式(23)中的x(a)和y(a)以及式(24)代入式(22)可得 (25) 式中 命題1假設(shè)ψ(a,τ)>0,?0≤τ≤σ≤a,則 1)J(ω)是關(guān)于ω單調(diào)遞減的函數(shù),并且 2)J(0)<1. 證明根據(jù)式(25)和ψ(a,τ)>0可知: J(ω)≥0,J′(ω)<0 在式(25)中,令ω=0,則 (26) 由式(19)可知,式(26)的第一項等于1,所以J(0)<1. 定理4若R0>1,ψ(a,τ)>0,?0≤τ≤σ≤a,則模型(3)的地方病平衡態(tài)是局部漸近穩(wěn)定的. 證明類似于定理1的證明.若R0>1,ψ(a,τ)>0,則J(ω)=1存在唯一的負實根,并且所有復根都具有負實部.因此,當R0>1時,模型(3)的地方病平衡態(tài)是局部漸近穩(wěn)定的. 迄今為止,已經(jīng)發(fā)展了許多數(shù)值方法來逼近偏微分方程組的解.利用有限差分法沿特征線離散化模型(1),并進行數(shù)值模擬.假設(shè)模型基本參數(shù)如下: γ(a)=0.48sin2(0.1πa) θ(a)=0.26sin2(0.1πa) δ(a)=0.15sin2(0.1πa) ξ(a)=0.5×10-3sin2(0.1πa) 討論模型的主要參數(shù)對基本再生數(shù)R0的影響,選擇參數(shù)k(a)=0.2e-0.01a,β1(a)=0.000 11e-0.04a,β2(a)=0.075e-0.02a.根據(jù)R0的表達式,R0與接觸率k(a)和傳染率βj(a) (j=1,2)是正相關(guān)的.這也正如圖1a所示,R0隨著k(a)和β1(a)的增加而增加.此外,圖1b表明,當k(a)固定時,可以通過降低β1(a)來降低R0.因此,適當減少接觸并降低傳染率是控制霍亂傳播的有效措施之一. 圖1 R0關(guān)于k(a)和β1(a)的敏感性 選擇參數(shù)k(a)=0.9e-2a,β1(a)=0.000 11e-2a,β2(a)=0.075e-a,則計算可知R0≈0.402 1<1.根據(jù)定理2,無病平衡態(tài)E0是全局漸近穩(wěn)定的.此時,易感者和感染者的密度分布如圖2所示.特別地,當a=20時,對于不同的初值,S(t,20)隨著t趨于無窮而趨于1,I(t,20)隨著t趨于無窮而趨于0.這意味著,無論霍亂暴發(fā)的初始狀態(tài)如何,最終都會滅絕. 圖2 無病平衡態(tài)的穩(wěn)定性,R0<1 選擇參數(shù)k(a)=0.9e-a,β1(a)=0.000 11e-0.6a,β2(a)=0.075e-0.4a,則基本再生數(shù)R0≈1.426>1.由定理3可知,模型存在唯一的地方病平衡態(tài)E*.圖3表明,地方病平衡態(tài)E*是局部漸近穩(wěn)定的,當a=20時,對于不同的初值,I(t,20)隨著t趨于無窮而趨于地方病平衡態(tài).類似的,當t趨于無窮時,S(t,a),R(t,a),P(t,a)的密度分布會趨于地方病平衡態(tài).這意味著,霍亂將持續(xù)存在. 圖3 地方病平衡態(tài)E*的穩(wěn)定性,R0>1 基于霍亂弧菌傳播方式的多樣性和種群的異質(zhì)性,提出了一類具有生理年齡和環(huán)境傳播的霍亂弧菌在人和人之間,人與環(huán)境之間傳播的動力學模型,這里環(huán)境中霍亂弧菌也引入了年齡結(jié)構(gòu)以刻畫脫落的霍亂弧菌的活性.進一步利用半群理論,線性近似,比較原理等方法,獲得了模型全局正解的存在性與唯一性,以及疾病基本再生數(shù)的精確表達式,證明了當基本再生數(shù)小于1時,無病平衡態(tài)是全局漸近穩(wěn)定的; 而當基本再生數(shù)大于1時,無病平衡態(tài)是不穩(wěn)定的,模型存在唯一的地方病平衡態(tài),并在特定條件下得到其漸近穩(wěn)定性.如何得到不帶附加條件的地方病平衡態(tài)的局部或全局漸近穩(wěn)定性,是進一步值得考慮的問題.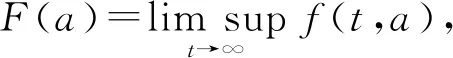
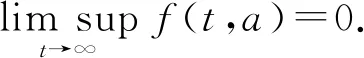
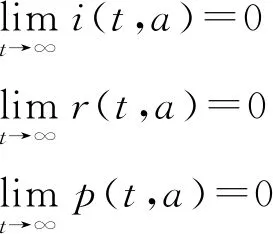
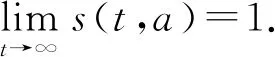
3 地方病平衡態(tài)的存在性與穩(wěn)定性
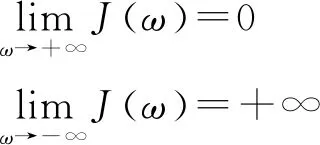
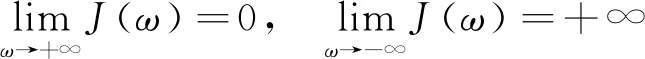
4 數(shù)值模擬
5 結(jié)論

