廣東省東莞市第一中學(xué)(523128)江明

平面解析幾何問題一直是高考命題的熱點和重點之一,而圓錐曲線大題作為高考必考題型,其考查的知識點覆蓋廣泛而細致,所涉及的數(shù)學(xué)思想內(nèi)涵極為豐富,解題思路多樣,主要考查學(xué)生的數(shù)學(xué)抽象,邏輯推理,直觀想象,數(shù)學(xué)運算和數(shù)據(jù)分析等核心素養(yǎng).由于高考中圓錐曲線大題往往位于試卷倒數(shù)第二題的位置, 對學(xué)生來說, 時間緊, 難度普遍較大,對計算能力的要求又較高,很多考生心生畏懼,束手無策,進而習(xí)慣性選擇放棄.本文將以化斜為直這一數(shù)學(xué)思想在圓錐曲線問題中的應(yīng)用為切入點,以一道高考真題為例,以點帶面, 探究在求解圓錐曲線問題中運用合適的數(shù)學(xué)思想解題,從而達到化繁為簡,簡化運算,事半功倍,輕松解題的目的.

1 真題再現(xiàn)

1.1 引例

(2010 北京卷理19)在平面直角坐標(biāo)系xoy中,點B與點A(-1,1)關(guān)于原點O對稱,P是動點,且直線AP與BP的斜率之積等于.

(1)求動點P的軌跡方程;

(2)設(shè)直線AP與BP分別與直線x= 3 交于點M,N,問: 是否存在點P使得ΔPAB與ΔPMN的面積相等? 若存在,求出點P的坐標(biāo);若不存在,說明理由.

1.2 分析

求解圓錐曲線問題的三個難點: 準(zhǔn)確作圖,分析與轉(zhuǎn)化問題,強大的計算能力,而分析與轉(zhuǎn)化問題尤為重要,直接決定了求解該問題的走向和難易程度.

思路一問(1)易得動點P的軌跡方程為;問(2)一步步來,如圖1,設(shè)P,表示BP和AP,求N,M,求|MN|,再求SΔPMN和SΔPAB,最后求出P.

詳解設(shè)點P的坐標(biāo)為(x0,y0),點M,N得坐標(biāo)分別為(3,yM),(3,yN).則直線AP的方程為,直線BP的方程為.令x= 3 得.于是ΔPMN的面積,又直線AB的方程為x+y= 0,, 點P到直線AB的距離.于是ΔPAB的面積.當(dāng)SΔPAB=SΔPMN時,得,又|x0+y0|0,所以,解得.因為,所以,故存在點P使得ΔPAB與ΔPMN的面積相等,此時點P的坐標(biāo)為.

思路二設(shè)直線AB與直線x= 3 的交點為K, 連接BM與AN, 如圖2, 由直線AB方程為x+y= 0, 點K在x= 3 上, 易得點K坐標(biāo)為(3,-3), 從而點B(1,-1)為AK的中點, 由SΔPMN=SΔPAB可得|PA|·|PB| =|PM| · |PN|, 即

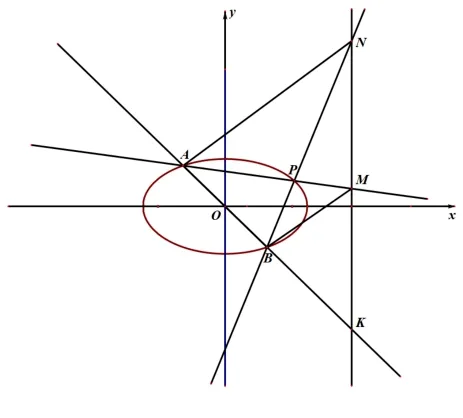
圖2

,

然后得到ΔPAN與ΔPBM相似, 從而AN//BM, 點M為KN的中點, 根據(jù)三角形重心的定義, 可知點P為ΔAKN的重心, 由三角形重心坐標(biāo)公式可得, 再根據(jù)可求得,故存在點P使ΔPAB與ΔPMN的面積相等,此時點P的坐標(biāo)為.

思路三抓住兩個三角形有角對頂,∠APB= ∠NPM,如圖3,由SΔPMN=SΔPAB可得,化斜為直:,從而求出P.

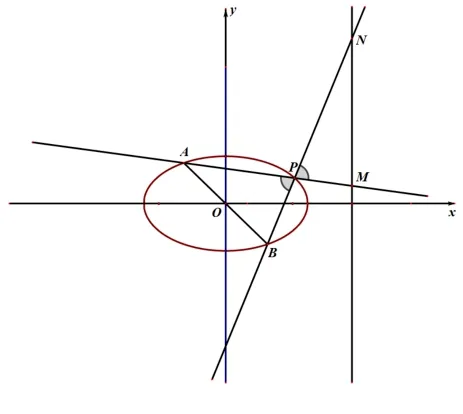
圖3

詳解若存在點P使得ΔPAB與ΔPMN的面積相等,設(shè)點P的坐標(biāo)為(x0,y0),則:.因為sin ∠APB= sin ∠MPN,所以, 所以即, 解得, 因為所以,故存在點P使得ΔPAB與ΔPMN的面積相等,此時點P的坐標(biāo)為.

1.3 小結(jié)

從這道2010 年高考北京卷理19 的三種解題方法可以看出,思路一審題浮于淺層,導(dǎo)致運算繁瑣,思路二需要深入分析圖形,思維容量大,對考生的知識儲備,觀察分析和作圖能力要求較高,而思路三適當(dāng)轉(zhuǎn)化條件,通過化斜為直,把斜線段之比轉(zhuǎn)化為直線段之比,化簡為繁,快刀斬亂麻,極大的簡化了運算,縮短了解題時間.

2 模擬精析

2.1 例題

(1)求雙曲線C的方程;

(2)過點P(0,3)的直線l與雙曲線C的右支交于不同的兩點A和B, 若直線l上存在不同于點P的點D滿足|PA|·|DB| = |PB|·|DA|成立,證明: 點D的縱坐標(biāo)為定值,并求出該定值.

2.2 分析

判斷點D的位置很關(guān)鍵,若點D在AB延長線上,如圖4,此時|PA|·|DB| ＜|PB|·|DA|,不符合題意,若點D在BA延長線上,如圖5,此時,這與題設(shè)相矛盾,不符合題意,故點D只能在A與B之間,如圖6 所示:

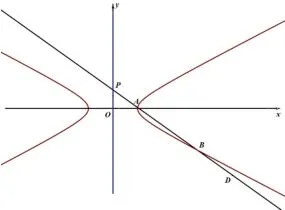
圖4

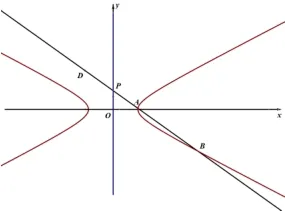
圖5

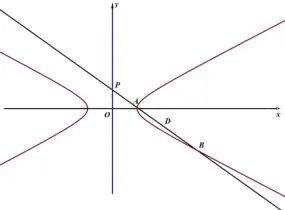
圖6

詳解問(1) 易得; 問(2) 設(shè)A(x1,y1),B(x2,y2),D(x0,y0),直線l的方程為y=kx+3.將直線方程y=kx+3 代入(1)中雙曲線方程,化簡整理得(1-4k2)x2-24kx-52 = 0,Δ = (-24k)2+4×(1-4k2)×52=208-256k2,則, 要使直線與雙曲線的右支有兩個不同的交點A和B, 則滿足解得, 由|PA| · |DB| = |PB| · |DA|,得, 化斜為直, 故, 所以, 又,所以點D的縱坐標(biāo)為定值.

2.3 小結(jié)

該題主要考查化斜為直數(shù)學(xué)思想,采用化斜為直方法的典型特征是題干中出現(xiàn)或者隱含了等價線段比關(guān)系,但有時需通過作圖綜合分析確定線段比關(guān)系才能準(zhǔn)備轉(zhuǎn)化,以免造成解題失誤.

3 鞏固提高

3.1 思考題

(1)求C的方程;

3.2 解析

問(1) 略, 易得C方程為; 問(2) 作圖有兩種情況, 以圖7 為例, 由題意, 可設(shè),則|t| ＜ 3, 且,G(x1,y1),H(x2,y2).直線.由得, 所以.

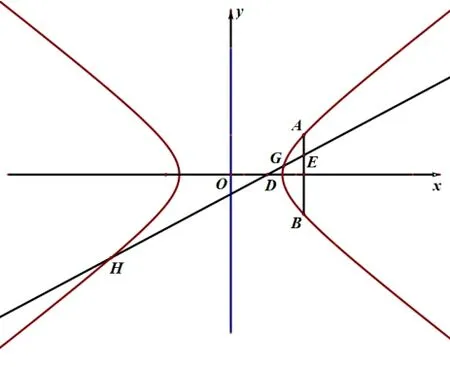
圖7

圖8

思路1:化斜為直

4 總結(jié)

化斜為直作為求解圓錐曲線問題的重要解題思想,當(dāng)題干中出現(xiàn)或者隱含了等價線段比關(guān)系時,通過化斜為直,把斜線段之比轉(zhuǎn)化為直線段之比,往往能夠達到化繁為簡,化抽象為具體,簡化運算,從而縮短解題時間,但有時也需通過作圖,認真分析,確定準(zhǔn)確的線段比關(guān)系,才能確保解題的準(zhǔn)確性.