劉春苔,李澤芳

(1.武漢工業(yè)學院數理科學系,湖北武漢 430023;2.武漢職業(yè)技術學院計算機系,湖北武漢 430047)

關于 Bernoulli卷積的一個譜性質

劉春苔1,李澤芳2

(1.武漢工業(yè)學院數理科學系,湖北武漢 430023;2.武漢職業(yè)技術學院計算機系,湖北武漢 430047)

設μρ是 R上的參數為 0＜ρ＜1的 Bernoulli卷積測度.Hu和 Lau證明了 L2(μ)空間中含有一個無限指數型正交序列的充要條件是ρ是分數 p/q的方根,其中 p為奇數,q為偶數.本文討論當ρ為其余情形時,指數型正交序列集中元素個數,證明了當ρ-1不是奇數型方程的根或者其本原最小多項式 g(x)滿足 g(l)為奇數時,則 L2(μ)中任何指數型正交集至多含有兩個元素.

Bernoulli卷積測度;最小本原多項式;正交集

設μ是 R上的一個 Borel概率測度.稱μ為一個譜測度,如果存在一個離散集合Λ使得集 E(λ)={e2π/λ(·)：λ∈Λ}為 L2(μ)的一個正交基 ,此時稱Λ為 μ的譜,(μ,Λ)為譜對. 因為 (μ,Λ)為譜對當且僅當對任意實數 t,(μ,Λ+t)為譜對,故為了簡潔性,可以假定 0∈Λ.譜測度最初是 Jorgensen和Pedersen[1]提出的,他們證明了：

定理 1設 k＞2為整數,μ為 R上 1/k-Cantor測度,則μ為譜測度當且僅當 k為奇數.進一步,如果 k為偶數,則 L2(μ)中任何正交集 E(Λ)中至多含有兩個元素.

對任意 Borel集 A?R,0＜ρ＜1,稱下式所定義的測度μ=μρ為 Bernoulli卷積測度

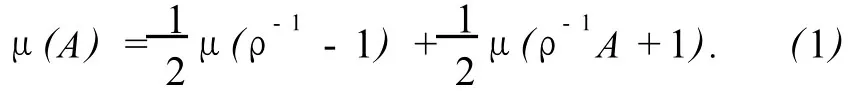
注意到上述定理中的 Cantor測度μ=μρ是 Bernoulli卷積測度μ的特殊情形,而對 Bernoulli卷積測度的研究已經有了很長的歷史了[2-5]：0＜ρ＜1/2時為Cantor型測度;1/2＜ρ＜1時為有重疊情形.Laba和Wang[6-7]將定理 1推廣到一般的 Borel測度.Strichartz[8-10]考慮了這種譜 Cantor測度的 Fourier級數和 Fourier變換.Hu和 Lau[11]考慮了滿足式(1.1)的 Bernoulli卷積測度,其中參數ρ∈(0,1),他們證明了如下定理.

定理 2設μ=μρ為式 (1)所定義的ρ-Bernoulli卷積測度,則 L2(μ)包含一個無限正交指數型序列集 E(λ)的充要條件是ρ為 p/q的 n次方根,這里 p為奇數,q為偶數.

稱下面的代數方程為奇數型方程

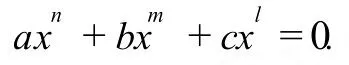
其中 a,b,c為奇數,m,n,l為非負整數.本文討論當ρ不是 p/q的 n次方根 (p為奇數,q為偶數)時,正交集 E(Λ)中所含元素的個數,我們得到如下定理：

定理 3設ρ-1的最小本原多項式為 g(x),若g(l)為偶數或者ρ-1為奇數型方程的根,則 L2(μ)中的任何正交集 E(Λ)至多含有兩個元素.

設μ為式 (1.1)所定義,則其 Fourier變換為

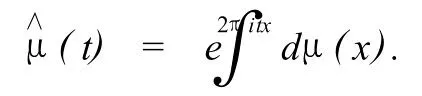
記β=ρ-1.在文[11]給出了下面兩個引理.

引理 1設 G為μ∧(t)的零點集,則 G={t=aβj/4：其中 a為奇數,j為正整數}且 G=-G.證明：對式 (1.1)兩邊進行 Fourier變換得

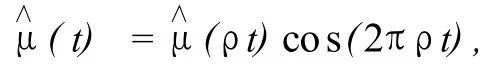
無限迭代下去,得

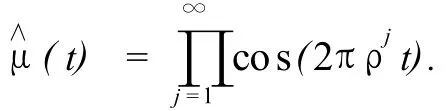
由于ρ∈(0,1),則對于任何 t,存在充分大的 J使得當 j ＞ J時,|2π ρjt| ＜π/2,于是 ,|cos(2π ρjt)|＞0.考慮到級數的通項與(π ρjt)2/2是等價無窮小,而后者所形成的級數在 R上內閉一致絕對收斂,于是上述級數在 t=0處連續(xù),從而(t)在零點連續(xù).考慮到(0)=1,并且j趨于無窮時 ρj趨于 0,從而(t)的零點集為cos(2π ρjt)零點集的并,即 G={t=aβj/4}其中 a為奇數,j為正整數.后一結論成立因為 cost是偶函數.

引理 2設 0∈Λ是一個離散集.則 E(λ)為L2(μ)的正交集當且僅當 (Λ -Λ)|{0}? G.進一步,Λ|{0}∈G.

證明：集 E(Λ)為正交集當且僅當對于λ,λ′∈Λ,λ ≠λ′有

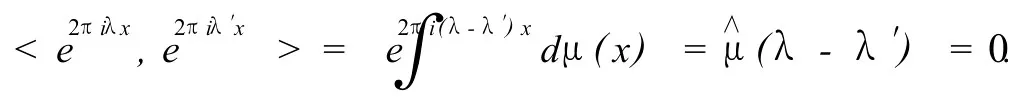
這就等價于λ-λ′∈G.而后一結論成立是因為 0∈Λ.

2 主要結果的證明

引理 3如果β＞1不是奇數型方程的解,則L2(μ)中正交集 E(Λ)至多含有兩個元素.

證明：設 #E(Λ)≥3.在Λ中任取兩個不等的非零元λ,λ′.由引理 2知λ-λ′∈G.而由引理 1可知存在奇數 a,b,c和非負整數m,n,l使得λ =aβm,λ′=cβn且

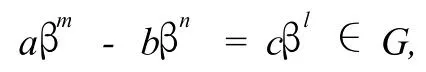
于是β是奇數型方程的解.

令Q[x]為有理系數多項式的全體,Z[x]為整系數多項式的全體.如果一個整系數多項式 f(x)的系數互素,則稱 f(x)為本原多項式.若它還是實數β的最小多項式,則稱其為最小本原多項式 (相對于β).下面的引理證明很簡單,可以在任何一本代數書上找到,故略過其證明.

引理 4設 g(x)∈Q[x]為β的最小多項式,f(x)∈Z[x]有一個實根β,則存在多項式 h(x)∈Z[x]和自然數 N,使得 f(x) =N g(x)h(x)且N g(x)∈Z[x]為β的最小本原多項式.

引理 5設β的本原最小多項式為 g(x),若g(l)偶數,則 L2(μ)的正交集 E(Λ)中至多含有兩個元素.

證明：由引理 3知,若 E(Λ)至少含有三個元,則β滿足某一奇數型方程記則 f(β)=0,從而存在整系數多項式 h(x),使得 f(x) =g(x)h(x).注意到f(l)=a+b+c為奇數,g(l)和 h(l)都為整數,則有 g(l)為奇數.

定理 3的證明：由引理 3和 5可知定理 3結論成立.

注：由引理5很容易得到定理1的必要性證明.事實上β=k為奇數的本原最小多項式為 g(x)=x-k,而 g(l)=1-k為偶數.

[1] Jorgensen P, Pedersen S. Dense analytic subspaces in fractal L2-spaces[J]. J Anal Math.1998,75：185-228.

[2] Falconer K.Fractal Geometry：Mathematical Foundations and Applications[M].Chichester：John Wiley&Sons,1990.

[3] Lau K S,Ngai SM.Multifractal measures and a weak separation condition[J]. Adv Math,1999,141：45-46.

[4] Lau K S,Ngai SM,Rao H.Iterated function systems with overlaps and self-similar measures[J].J London Math Soc.2001,63：249-268.

[5] Peres Y,Schlag W,Solomyak B.Sixty years of Bernoulli convolutions[J]. Progr Probab Birkhauser Basel,2000,46：39-65.

[6] Laba I,Wang Y.On spectral Cantor measures[J].J Funct Anal.2002,193：409-420.

[7] Laba I,Wang Y.Some properties of spectral measures[J].Appl Comput Harmon Anal,2006,20：149-157.

[8] Strichartz R. Remarks on“Denseanaly tic subspaces in fractal L2-spaces”by P.E.T.Jorgensen and S.Pedersen[J].J Anal Math,1998,75：229-231.

[9] Strichartz R.Mock Fourier series and transforms associated with certain Cantor measures[J].J Anal Math,2000,81：209-238.

[10] Strichartz R. Convergence of mock Fourier series[J].J Anal Math.2006,20：333-253.

[11] Hu Y T,Lau K S.Spectral property of the Bernoulli convolutions[J].Adv Math,2008,219：554– 567.

A spectral property of the Bernoulli convolutions

LIU Chun-tai1,LI Ze-fang2
(1.Department ofMathematics and Physics,Wuhan Polytechnic University,Wuhan 430023,China;2.Department of Computer,Wuhan Institute of Technology,Wuhan 430047,China)

Let be the Bernoulli convolution associated with on.Hu and Lau proved that the space contained an infinite orthonormal set of exponential functions if and only if is the nth root of a fraction where is odd and even.In this paper,we discuss the number of the orthonormal set of exponential function in other cases.And we prove that either isn't a root of a equation of“odd”type or is even,any orthonormal set of exponential function in has at most two elements,where is the minimal primitives polynomial for.

Bernoulli convolution;minimal primitives polynomial;orthonor mal set

O 174

A

1009-4881(2010)01-0103-02

10.3969/j.issn.1009-4881.2010.01.028

2009-06-25.

劉春苔 (1976-),女,碩士,E-mail：ct98-4@163.com.