空間型上的近Yamabe孤立子

陳佳蕊, 劉建成

(西北師范大學 數(shù)學與統(tǒng)計學院, 蘭州 730070)

1 引言與主要結(jié)果

若Riemann流形(Mn,g)上存在一個向量場v和一個常數(shù)λ, 使得(R-λ)g=Lvg/2, 則稱Riemann流形(Mn,g)為Yamabe孤立子, 記為(Mn,g,v,λ), 其中:v稱為孤子場;R表示流形Mn的數(shù)量曲率;Lvg表示流形Mn上度量g沿向量場v的李導數(shù);λ∈. 當λ>0(λ=0或λ<0)時, 稱Yamabe孤立子(Mn,g,v,λ)為收縮(穩(wěn)定或擴張)Yamabe孤立子. 若向量場v是流形Mn上一些光滑函數(shù)f的梯度, 則稱Yamabe孤立子(Mn,g,v,λ)為梯度Yamabe孤立子, 記為(Mn,g,f,ρ). Yamabe孤立子是Yamabe流的特解. 近年來, 關(guān)于Yamabe孤立子的研究已有很多成果[1-4]. 文獻[5]介紹了Yamabe孤立子的一個推廣, 即近Yamabe孤立子.

若Riemann流形(Mn,g)上存在一個向量場v和一個光滑函數(shù)ρ, 使得

(R-ρ)g=Lvg/2,

(1)

則稱Riemann流形(Mn,g)為近Yamabe孤立子, 記為(Mn,g,v,ρ), 其中:v稱為孤子場;ρ稱為孤子函數(shù);R表示流形Mn的數(shù)量曲率;Lvg表示流形Mn上度量g沿向量場v的李導數(shù). 若向量場v是流形Mn上一些光滑函數(shù)f的梯度, 則稱近Yamabe孤立子(Mn,g,v,ρ)為梯度近Yamabe孤立子, 記為(Mn,g,f,ρ). 當光滑函數(shù)ρ取常數(shù)時, 近Yamabe孤立子是Yamabe孤立子, 梯度近Yamabe孤立子是梯度Yamabe孤立子.

其中:V,W是流形Mn上的任意光滑切向量場;XN表示位置向量場X的法分量;R表示流形Mn的數(shù)量曲率;λ是一個常數(shù). 文獻[7]在相同的條件下, 將文獻[6]的結(jié)果推廣到了近Yamabe孤立子, 并得到了歐氏空間中超曲面上任意一個近Yamabe孤立子都被包含在超平面或球面中.

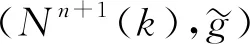
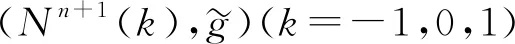
其中:V,W是流形Mm上的任意光滑切向量場;XN表示向量場X的法分量;R表示流形Mm的數(shù)量曲率;ρ表示流形Mm上任意一個光滑函數(shù), 此時記近Yamabe孤立子為(Mm,g,XT,ρ).

注1對定理1, 當φ(r)=r,r∈[0,∞), 即截曲率k=0時, 空間型Nn+1(k)是歐氏空間n+1, 此時定理1與文獻[7]中引理4.1的結(jié)果一致.

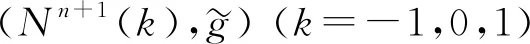
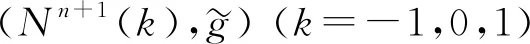
2 預備知識

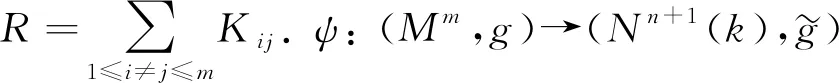
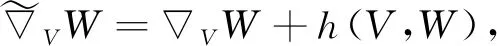
(2)

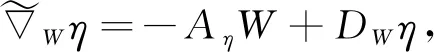
(3)

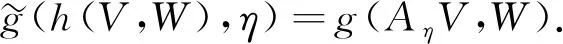
(4)

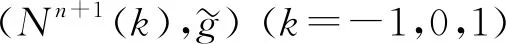
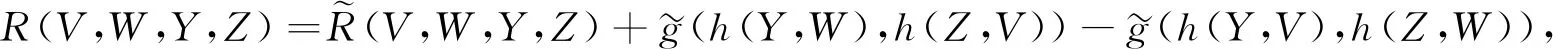
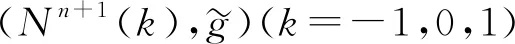
3 主要結(jié)果的證明

X=XT+XN.

(5)

3.1 定理1的證明

先證明必要性. 一方面, 子流形(Mm,g)是以向量場X的切分量XT作為孤子場的近Yamabe孤立子, 由式(1)可知, 切分量XT滿足

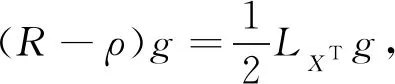
(6)

其中:R是子流形Mm的數(shù)量曲率;ρ是子流形Mm上的任意一個光滑函數(shù).

另一方面, 由引理1知, 對子流形Mm上的任意光滑切向量場Y, 向量場X滿足

(7)

代入式(5)可得

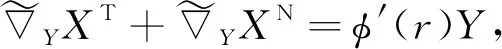
(8)

將式(8)代入式(2)和式(3)可得

φ′(r)Y=YXT+h(Y,XT)-AXNY+DYXN.

(9)

對比式(9)中的切分量和法分量, 有

YXT=φ′(r)Y+AXNY,

(10)

h(Y,XT)=-DYXN.

結(jié)合李導數(shù)的定義, 由式(4)和式(10)可知

其中V,W是子流形Mm上的任意光滑切向量場. 將式(11)與式(6)做對比可得

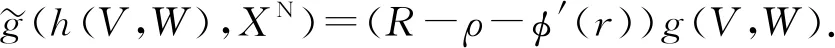
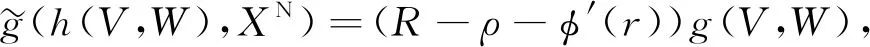
(12)

其中:V,W是子流形Mm上的任意光滑切向量場;R是子流形Mm的數(shù)量曲率;ρ是子流形Mm上任意一個光滑函數(shù). 當φ(r)=r,r∈[0,∞)時, 截曲率k=0; 當φ(r)=sinr,r∈[0,π)時, 截曲率k=1; 當φ(r)=sinhr,r∈[0,∞)時, 截曲率k=-1.

另一方面, 由上述必要性的證明可知

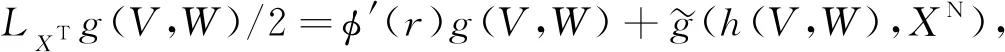
(13)

結(jié)合式(12)和式(13)可得(R-ρ)g=LXTg/2, 即子流形(Mm,g)是以向量場X的切分量XT為孤子場的近Yamabe孤立子.

3.2 推論1的證明

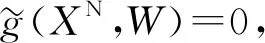
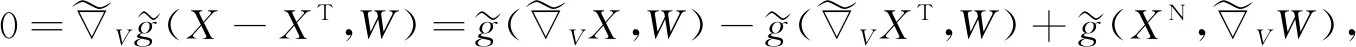
(14)

將式(14)代入式(2)和式(7)可得

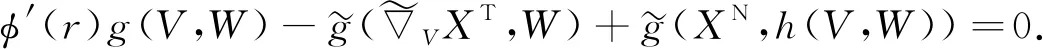
(15)

3.3 定理2的證明

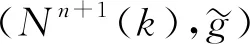
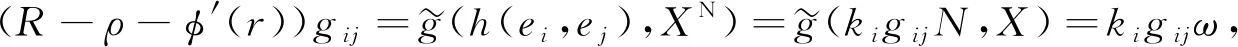
(16)

其中i,j=1,2,…,n. 由式(16)可得

R-ρ-φ′(r)=ωki,

(17)

對式(17)求和可得

R-ρ-φ′(r)=ωα,

(18)

比較式(17)和式(18), 有ki=α, 因此Mn是全臍超曲面, 定理2得證.