單 墫

(南京師范大學數(shù)學科學學院,210023)

一位名叫李雨航的朋友問下面的問題有無好的解法:

問題已知正實數(shù)a,b,c滿足

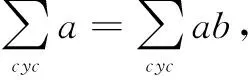
(1)

求證:

(2)

這道題已有好幾個解答,前面公布的解法都很精彩.我的解法與他們不同(所以還值得發(fā)一下),與李雨航倒有類似之處(但他的解法中,判別式Δ≤0的那步,我看不懂).

q≥2+r.

(2′)

不妨設(shè)a≥b≥c.當a=b=c=1時,(2′)式顯然成立.下設(shè)a,b,c不全為1.

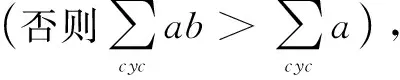
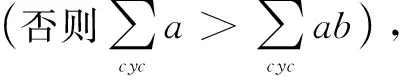
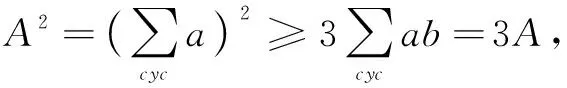
對于正實數(shù)x,y,z,有Schur不等式

(x+y+z)3-4(x+y+z)(xy+yz+zx)+9xyz≥0.

(3)

(參見拙著《數(shù)學競賽研究教程》習題17.12或《代數(shù)不等式的證明》例28)

取x=a,y=b,z=c,得A3-4A2+9r2≥0.因為A≥3,所以A3-4A2+A2r2≥0,從而

A≥4-r2.

(4)

在b≥1時,0≤(1-a)(1-b)(1-c)=1-A+A-r2=1-r2,所以

r≤1.

(5)

而

q2=A+2pr,

(6)

p2=A+2q,

(7)

所以q2-p2=2(pr-q)≤2(p-q),從而

p≥q.

(8)

再由(6),有q2≥A+2qr≥4-r2+2qr,從而(q-r)2≥4,q≥2+r.

在b<1時,(5)變?yōu)?/p>

r>1.

(5′)

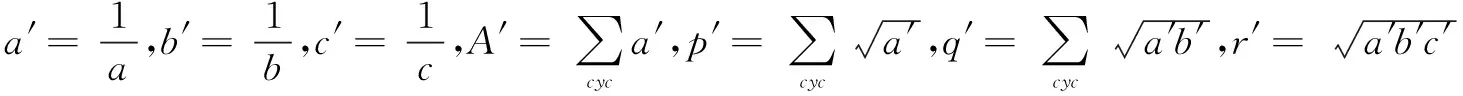
于是,同樣有p′≥q′≥2+r′≥1+2r′,兩邊同乘以r,即得q≥2+r.

注b<1的情況也可以不依賴于b≥1的情況直接證明.